
【题目】对于给定的正整数k,如果各项均为正数的数列{an}满足:对任意正整数n(n>k),an﹣kan﹣k+1…an﹣1an+1…an+k﹣1an+k=an2k总成立,那么称{an}是“Q(k)数列”.
(1)若{an}是各项均为正数的等比数列,判断{an}是否为“Q(2)数列”,并说明理由;
(2)若{an}既是“Q(2)数列”,又是“Q(3)数列”,求证:{an}是等比数列.
【答案】
(1)解:假设{an}是各项均为正数的等比数列,由等比数列的性质可得:an﹣2an﹣1an+1an+2=an﹣2an+2an﹣1an+1= ![]()
![]() =
= ![]() .
.
∴{an}为“Q(2)数列”
(2)证明:{an}既是“Q(2)数列”,又是“Q(3)数列”,
∴an﹣2an﹣1an+1an+2= ![]() .an﹣3an﹣2an﹣1an+1an+2an+3=
.an﹣3an﹣2an﹣1an+1an+2an+3= ![]() .
.
可得:an﹣3an+3= ![]() .对于任意n∈N*(n≥4)都成立.
.对于任意n∈N*(n≥4)都成立.
∴{an}是等比数列
【解析】(1)根据等比数列的性质an-1an+1=an2即可求证;(2)根据题意可知数列![]() 满足关系式an-2
满足关系式an-2![]() an-1
an-1![]() an+1
an+1![]() an+2=an4和an-3
an+2=an4和an-3![]() an-2
an-2![]() an-1
an-1![]() an+1
an+1![]() an+2
an+2![]() an+3=an6,两式相除可得an-3
an+3=an6,两式相除可得an-3![]() an+3=an2.
an+3=an2.
【考点精析】本题主要考查了等比数列的基本性质的相关知识点,需要掌握{an}为等比数列,则下标成等差数列的对应项成等比数列;{an}既是等差数列又是等比数列== {an}是各项不为零的常数列才能正确解答此题.


 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案科目:高中数学 来源: 题型:
【题目】某油库的设计容量是30万吨,年初储量为10万吨,从年初起计划每月购进石油m万吨,以满足区域内和区域外的需求,若区域内每月用石油1万吨,区域外前x个月的需求量y(万吨)与x的函数关系为y= ![]() (p>0,1≤x≤16,x∈N*),并且前4个月,区域外的需求量为20万吨.
(p>0,1≤x≤16,x∈N*),并且前4个月,区域外的需求量为20万吨.
(1)试写出第x个月石油调出后,油库内储油量M(万吨)与x的函数关系式;
(2)要使16个月内每月按计划购进石油之后,油库总能满足区域内和区域外的需求,且每月石油调出后,油库的石油剩余量不超过油库的容量,试确定m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥S﹣ABC中,SA=SC,AB⊥AC,D为BC的中点,E为AC上一点,且DE∥平面SAB.求证: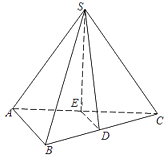
(1)直线AB∥平面SDE;
(2)平面ABC⊥平面SDE.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题p:x∈[2,4],x2﹣2x﹣2a≤0恒成立,命题q:f(x)=x2﹣ax+1在区间 ![]() 上是增函数.若p∨q为真命题,p∧q为假命题,求实数a的取值范围.
上是增函数.若p∨q为真命题,p∧q为假命题,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax2+(2a﹣1)x﹣lnx,a∈R.
(1)若曲线y=f(x)在点(1,f(1))处的切线经过点(2,11),求实数a的值;
(2)若函数f(x)在区间(2,3)上单调,求实数a的取值范围;
(3)设 ![]() ,若对x1∈(0,+∞),x2∈[0,π],使得f(x1)+g(x2)≥2成立,求整数a的最小值.
,若对x1∈(0,+∞),x2∈[0,π],使得f(x1)+g(x2)≥2成立,求整数a的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】观察下列各式: C ![]() =40;
=40;
C ![]() +C
+C ![]() =41;
=41;
C ![]() +C
+C ![]() +C
+C ![]() =42;
=42;
C ![]() +C
+C ![]() +C
+C ![]() +C
+C ![]() =43;
=43;
…
照此规律,当n∈N*时,
C ![]() +C
+C ![]() +C
+C ![]() +…+C
+…+C ![]() = .
= .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com