
 cm,∠ACB=60°,则球心O到平面ABC的距离为
cm,∠ACB=60°,则球心O到平面ABC的距离为 cm
cm cm,∠ACB=60°,由正弦定理可求得其外接圆的直径为
cm,∠ACB=60°,由正弦定理可求得其外接圆的直径为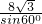 =16,即半径为8,由此几何体的结构特征知,用勾股定理求球心O到平面ABC的距离即可.
=16,即半径为8,由此几何体的结构特征知,用勾股定理求球心O到平面ABC的距离即可. cm,∠ACB=60°,
cm,∠ACB=60°,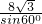 =16,即半径为8
=16,即半径为8

 计算高手系列答案
计算高手系列答案科目:高中数学 来源:2007-2008学年浙江省温州市十校联合体高三(上)期末数学试卷(文科)(解析版) 题型:填空题
查看答案和解析>>
科目:高中数学 来源:2007-2008学年浙江省温州市十校联合体高三(上)期末数学试卷(理科)(解析版) 题型:填空题
查看答案和解析>>
科目:高中数学 来源:2010-2011学年广东省珠海一中高三(下)第一次调研数学试卷(理科)(解析版) 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com