
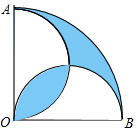
 如图,在圆心角为直角的扇形OAB中,分别以OA,OB为直径作两个半圆,设OA=1,则阴影部分的面积是$\frac{π-2}{4}$.
如图,在圆心角为直角的扇形OAB中,分别以OA,OB为直径作两个半圆,设OA=1,则阴影部分的面积是$\frac{π-2}{4}$. 分析 设两个半圆相交于点O,C.连接OC,OB.由$\frac{1}{4}×π×{1}^{2}$=$π×(\frac{1}{2})^{2}$,可得直角的扇形OAB的面积等于分别以OA、OB为直径作两个半圆的面积的和.由对称性可得:OC平分∠AOB.即可得出要求的阴影部分的面积.
解答 解:设两个半圆相交于点O,C.连接OC,OB.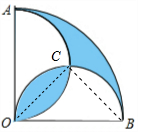
∵$\frac{1}{4}×π×{1}^{2}$=$π×(\frac{1}{2})^{2}$,
∴直角的扇形OAB的面积等于分别以OA、OB为直径作两个半圆的面积的和.
由对称性可得:OC平分∠AOB.
∴要求的阴影部分的面积S=2×$[\frac{1}{2}π×(\frac{1}{2})^{2}-\frac{1}{2}×(\frac{\sqrt{2}}{2})^{2}]$=$\frac{π-2}{4}$.
故答案为:$\frac{π-2}{4}$.
点评 本题考查了扇形的面积计算公式、圆的面积计算公式,考查了推理能力与计算能力,属于中档题.


 智慧小复习系列答案
智慧小复习系列答案科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
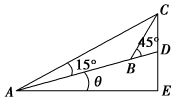 如图所示,在坡度一定的山坡A处测得山顶上一建筑物CD的顶端C对于山坡的斜度为15°,向山顶前进100m到达B处,又测得C对于山坡的斜度为45°,若CD=50m,山坡对于地平面的坡度为θ,则cosθ=$\sqrt{3}$-1.
如图所示,在坡度一定的山坡A处测得山顶上一建筑物CD的顶端C对于山坡的斜度为15°,向山顶前进100m到达B处,又测得C对于山坡的斜度为45°,若CD=50m,山坡对于地平面的坡度为θ,则cosθ=$\sqrt{3}$-1.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1024 | B. | 1023 | C. | 2048 | D. | 2046 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com