
【题目】选修4 — 4:坐标系与参数方程
在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为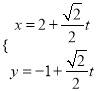 (
(![]() 为参数),以原点为极点,
为参数),以原点为极点, ![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() (
(![]() ).
).
(1)分别写出直线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)已知点![]() ,直线
,直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 两点,若
两点,若![]() ,求
,求![]() 的值.
的值.
科目:高中数学 来源: 题型:
【题目】已知点![]() 为抛物线
为抛物线![]() 内一定点,过
内一定点,过![]() 作两条直线交抛物线于
作两条直线交抛物线于![]() ,且
,且![]() 分别是线段
分别是线段![]() 的中点.
的中点.
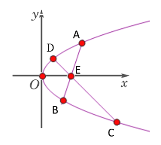
(1)当![]() 时,求△
时,求△![]() 的面积的最小值;
的面积的最小值;
(2)若![]() 且
且![]() ,证明:直线
,证明:直线![]() 过定点,并求定点坐标。
过定点,并求定点坐标。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率是
的离心率是![]() ,且椭圆经过点
,且椭圆经过点![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若直线![]() :
: ![]() 与圆
与圆![]() 相切:
相切:
(ⅰ)求圆![]() 的标准方程;
的标准方程;
(ⅱ)若直线![]() 过定点
过定点![]() ,与椭圆
,与椭圆![]() 交于不同的两点
交于不同的两点![]() ,与圆
,与圆![]() 交于不同的两点
交于不同的两点![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,![]() 为平行四边形ABCD所在平面外一点,M,N分别为AB,PC的中点,平面PAD
为平行四边形ABCD所在平面外一点,M,N分别为AB,PC的中点,平面PAD![]() 平面PBC=
平面PBC=![]() .
.
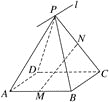
(1)求证:BC∥![]() ;
;
(2)MN与平面PAD是否平行?试证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知 (
(![]() ,
, ![]() )展开式的前三项的二项式系数之和为16,所有项的系数之和为1.
)展开式的前三项的二项式系数之和为16,所有项的系数之和为1.
(1)求![]() 和
和![]() 的值;
的值;
(2)展开式中是否存在常数项?若有,求出常数项;若没有,请说明理由;
(3)求展开式中二项式系数最大的项.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地级市共有200000中小学生,其中有7%学生在2017年享受了“国家精准扶贫”政策,在享受“国家精准扶贫”政策的学生中困难程度分为三个等次:一般困难、很困难、特别困难,且人数之比为5:3:2,为进一步帮助这些学生,当地市政府设立“专项教育基金”,对这三个等次的困难学生每年每人分别补助1000元、1500元、2000元。经济学家调查发现,当地人均可支配年收入较上一年每增加n%,一般困难的学生中有3n%会脱贫,脱贫后将不再享受“精准扶贫”政策,很困难的学生中有2n%转为一般困难,特别困难的学生中有n%转为很困难。现统计了该地级市2013年到2017年共5年的人均可支配年收入,对数据初步处理后得到了如图所示的散点图和表中统计量的值,其中年份![]() 取13时代表2013年,
取13时代表2013年, ![]() 与
与![]() (万元)近似满足关系式
(万元)近似满足关系式![]() ,其中
,其中![]() 为常数。(2013年至2019年该市中学生人数大致保持不变)
为常数。(2013年至2019年该市中学生人数大致保持不变)


其中![]() ,
, ![]()
(Ⅰ)估计该市2018年人均可支配年收入;
(Ⅱ)求该市2018年的“专项教育基金”的财政预算大约为多少?
附:①对于一组具有线性相关关系的数据![]() ,其回归直线方程
,其回归直线方程
![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为
②
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com