Question

【题目】椭圆 =1上有一点M（﹣4， ）在抛物线y2=2px（p＞0）的准线l上，抛物线的焦点也是椭圆焦点．
（1）求椭圆的标准方程；
（2）若点N在抛物线上，过N作准线l的垂线，垂足为Q，求|MN|+|NQ|的最小值．

Answer 1

【答案】
（1）解：∵ =1上的点M在抛物线y2=2px（p＞0）的准线l上，抛物线的焦点也是椭圆焦点．

∴c=﹣4，p=8…①

∵M（﹣4， ）在椭圆上，∴ …②

又∵a2=b2+c2…③

∴由①②③解得：a=5、b=3，

∴椭圆为 ；

由p=8得抛物线为y2=16x

（2）解：设椭圆焦点为F（4，0），由椭圆定义得|NQ|=|NF|，

∴|MN|+|NQ|=|MN|+|NF|≥|MF|= ，即为所求的最小值．

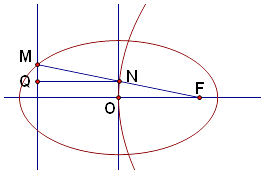
【解析】（1）由题意求得c=﹣4，得到p=8，再由点M（﹣4， ）在椭圆上，结合隐含条件求得a，b的值，则椭圆方程和抛物线方程可求；（2）由题意画出图形，由抛物线定义把|MN|+|NQ|的最小值转化为|MF|求解．