
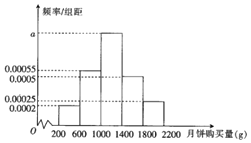
【题目】2018年中秋节到来之际,某超市为了解中秋节期间月饼的销售量,对其所在销售范围内的1000名消费者在中秋节期间的月饼购买量![]() 单位:
单位:![]() 进行了问卷调查,得到如下频率分布直方图:
进行了问卷调查,得到如下频率分布直方图:
![]() 求频率分布直方图中a的值;
求频率分布直方图中a的值;
![]() 以频率作为概率,试求消费者月饼购买量在
以频率作为概率,试求消费者月饼购买量在![]() 的概率;
的概率;
![]() 已知该超市所在销售范围内有20万人,并且该超市每年的销售份额约占该市场总量的
已知该超市所在销售范围内有20万人,并且该超市每年的销售份额约占该市场总量的![]() ,请根据这1000名消费者的人均月饼购买量估计该超市应准备多少吨月饼恰好能满足市场需求
,请根据这1000名消费者的人均月饼购买量估计该超市应准备多少吨月饼恰好能满足市场需求![]() 频率分布直方图中同一组的数据用该组区间的中点值作代表
频率分布直方图中同一组的数据用该组区间的中点值作代表![]() ?
?
科目:高中数学 来源: 题型:
【题目】已知直线![]() 与圆锥曲线C相交于A,B两点,与
与圆锥曲线C相交于A,B两点,与![]() 轴、
轴、![]() 轴分别交于D、E两点,且满足
轴分别交于D、E两点,且满足![]() .
.
(1)已知直线![]() 的方程为
的方程为![]() ,且A的横坐标小于B的横坐标,抛物线C的方程为
,且A的横坐标小于B的横坐标,抛物线C的方程为![]() ,求
,求![]() 的值;
的值;
(2)已知双曲线![]() ,求点D的坐标.
,求点D的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了对某课题进行研究,用分层抽样方法从三所高校A,B,C的相关人员中,抽取若干人组成研究小组、有关数据见下表(单位:人)
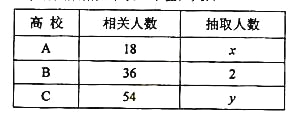
(I) 求x,y ;
(II) 若从高校B、C抽取的人中选2人作专题发言,求这二人都来自高校C的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将正方形ABCD沿对角线BD折成直二面角A-BD-C,有如下四个结论
①AC⊥BD;
②△ACD是等边三角形;
③AB与平面BCD成60°的角;
④AB与CD所成的角是60°.
其中正确结论的序号是________
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以直角坐标系xOy的坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C1的极坐标方程是![]() ,曲线C2的参数方程是
,曲线C2的参数方程是![]() (θ为参数).
(θ为参数).
(1)写出曲线C1,C2的普通方程;
(2)设曲线C1与y轴相交于A,B两点,点P为曲线C2上任一点,求|PA|2+|PB|2的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了迎接2019年全国文明城市评比,某市文明办对市民进行了一次文明创建知识的网络问卷调查.每一位市民有且仅有一次参加机会,通过随机抽样,得到参加问卷调查的1000人的得分(满分:100分)数据,统计结果如下表所示:
组别 |
|
|
|
|
|
|
|
频数 | 25 | 150 | 200 | 250 | 225 | 100 | 50 |
(1)由频数分布表可以认为,此次问卷调查的得分![]() 服从正态分布
服从正态分布![]() ,
,![]() 近似为这1000人得分的平均值(同一组数据用该组区间的中点值作为代表),请利用正态分布的知识求
近似为这1000人得分的平均值(同一组数据用该组区间的中点值作为代表),请利用正态分布的知识求![]() ;
;
(2)在(1)的条件下,文明办为此次参加问卷调查的市民制定如下奖励方案:
(i)得分不低于![]() 的可以获赠2次随机话费,得分低于
的可以获赠2次随机话费,得分低于![]() 的可以获赠1次随机话费;
的可以获赠1次随机话费;
(ii)每次获赠的随机话费和对应的概率为:
获赠的随机话费(单位:元) | 20 | 40 |
概率 |
|
|
现市民小王要参加此次问卷调查,记![]() (单位:元)为该市民参加问卷调查获赠的话费,求
(单位:元)为该市民参加问卷调查获赠的话费,求![]() 的分布列及数学期望.
的分布列及数学期望.
附:①![]() ;
;
②若![]() ,则
,则![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年世界服装市场是富有经济活力的一年,某国有企业为了使2019年服装效益更上一层楼,决定进一步深化企业改革、制定好的政策,为此,该企业对某品牌服装2018年1月份~5月份的销售量![]() (万件)与利润
(万件)与利润![]() (万元)作统计数据如下表:
(万元)作统计数据如下表:
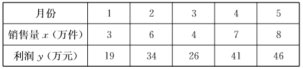
(1)从这![]() 个月的利润(单位:万元)中任选
个月的利润(单位:万元)中任选![]() 个月,求此
个月,求此![]() 个月利润均大于
个月利润均大于![]() 万元且小于
万元且小于![]() 万元的概率;
万元的概率;
(2)已知销售量![]() (万件)与利润
(万件)与利润![]() (万元)大致满足线性相关关系,请根据前
(万元)大致满足线性相关关系,请根据前![]() 个月的数据,求出
个月的数据,求出![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(3)若由线性回归方程得到的利润的估计数据与真实数据的误差不超过![]() 万元,则认为得到的利润的估计数据是理想的.请用表格中第
万元,则认为得到的利润的估计数据是理想的.请用表格中第![]() 个月的数据检验由(2)中回归方程所得的第
个月的数据检验由(2)中回归方程所得的第![]() 个月的利润的估计数据是否理想.
个月的利润的估计数据是否理想.
注:![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com