练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知函数，则的单调递减区间为（   ）

    A．[0，1） B．（-∞，0）
    C． D．（-∞，1）和（1，+∞）

    D

    解析试题分析:的单调递减区间是和，那么，根据复合函数的定义，知的单调递减区间：和,解得：和,所以单调递减区间是（-∞，1）和（1，+∞），故选D.
    考点：复合函数单调性

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：单选题

    如图放置的边长为1的正方形沿轴正方向滚动.设顶点的轨迹方程是，设在其两个相邻零点间的图象与轴所围区域为S,则直线从所匀速移动扫过区域S的面积D与的函数图象大致为（    ）．

     
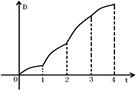
    A.                    B.                    C.                    D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    设函数，若和是函数的两个零点，和是的两个极值 点，则等于(      )

    A．B．C．D．

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    已知函数y=f(x)满足:对任意的x1<x2≤-1,[f(x2)-f(x1)](x2-x1)>0恒成立,则f(-2),f(-),f(-1)的大小关系为(　　)

    A．f(-2)<f(-)<f(-1)
    B．f(-2)>f(-)>f(-1)
    C．f(-2)>f(-1)>f(-)
    D．f(-)>f(-2)>f(-1)

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    已知函数f(x)＝ (k∈R)，若函数y＝|f(x)|＋k有三个零点，则实数k的取值范围是(　　)

    A．k≤2 B．－1<k<0 C．－2≤k<－1 D．k≤－2

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    函数y＝的图象大致是 (　　)．

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    已知函数y＝f(x)是定义在R上的奇函数，且当x<0时，不等式f(x)＋xf′(x)<0成立，若a＝30.3f(30.3)，b＝logπ3f(logπ3)，c＝log3f，则a，b，c间的大小关系是(　　)．

    A．a>b>c B．c>b>a 
    C．c>a>b D．a>c>b 

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    若函数y＝f(x)(x∈R)满足f(x＋1)＝－f(x)，且x∈[－1,1]时f(x)＝1－x2.函数g(x)＝则函数h(x)＝f(x)－g(x)在区间[－5,4]内的零点的个数(　　)．

    A．7 B．8?，
    C．9 D．10

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    若曲线f(x，y)＝0上两个不同点处的切线重合，则称这条切线为曲线f(x，y)＝0的“自公切线”．下列方程：①x2－y2＝1；②y＝x2－|x|，③y＝3sin x＋4cos x；④|x|＋1＝对应的曲线中存在“自公切线”的有(　　)．

    A．①②B．②③C．①④D．③④

    查看答案和解析>>

    同步练习册答案