
【题目】已知函数![]() ,曲线
,曲线![]() 在点
在点![]() 处的切线与直线
处的切线与直线![]() 垂直(其中
垂直(其中![]() 为自然对数的底数).
为自然对数的底数).
(Ⅰ)求![]() 的解析式及单调递减区间;
的解析式及单调递减区间;
(Ⅱ)若函数![]() 无零点,求
无零点,求![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)单调减区间为![]() 和
和![]() ;(Ⅱ)
;(Ⅱ) ![]() 的取值范围为:
的取值范围为: ![]() 或
或![]() .
.
【解析】试题分析:
(Ⅰ)利用切线求出参数![]() 值为2,解不等式
值为2,解不等式![]() 可得减区间;
可得减区间;
(Ⅱ)函数![]() 无零点,即方程
无零点,即方程![]() 在
在![]() 内无解,亦即要
内无解,亦即要![]() 在
在![]() 内无解.为此构造函数
内无解.为此构造函数![]() ,利用导数研究
,利用导数研究![]() 的单调性,可得结论,注意对
的单调性,可得结论,注意对![]() 分类讨论
分类讨论
试题解析:
(Ⅰ)解:![]() ,
,
又由题意有:![]()
![]() ,故
,故![]() .
.
此时,![]() ,由
,由![]() 或
或![]() ,
,
所以函数![]() 的单调减区间为
的单调减区间为![]() 和
和![]() .
.
(Ⅱ)解:
![]()
![]() ,且定义域为
,且定义域为![]() ,
,
要函数![]() 无零点,即要
无零点,即要![]() 在
在![]() 内无解,
内无解,
亦即要![]() 在
在![]() 内无解.
内无解.
构造函数![]() .
.
①当![]() 时,
时,![]() 在
在![]() 内恒成立,所以函数
内恒成立,所以函数![]() 在
在![]() 内单调递减,
内单调递减,![]() 在
在![]() 内也单调递减.又
内也单调递减.又![]() ,所以在
,所以在![]() 内无零点,
内无零点,
在![]() 内也无零点,故满足条件;
内也无零点,故满足条件;
②当![]() 时,
时,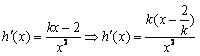
⑴若![]() ,则函数
,则函数![]() 在
在![]() 内单调递减,在
内单调递减,在![]() 内也单调递减,在
内也单调递减,在![]() 内单调递增.又
内单调递增.又![]() ,所以在
,所以在![]() 内无零点;易知
内无零点;易知![]() ,而
,而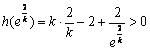 ,故在
,故在![]() 内有一个零点,所以不满足条件;
内有一个零点,所以不满足条件;
⑵若![]() ,则函数
,则函数![]() 在
在![]() 内单调递减,在
内单调递减,在![]() 内单调递增.又
内单调递增.又![]() ,所以
,所以![]() 时,
时,![]() 恒成立,故无零点,满足条件;
恒成立,故无零点,满足条件;
⑶若![]() ,则函数
,则函数![]() 在
在![]() 内单调递减,在
内单调递减,在![]() 内单调递增,在
内单调递增,在![]() 内也单调递增.又
内也单调递增.又![]() ,所以在
,所以在![]() 及
及![]() 内均无零点.
内均无零点.
又易知![]() ,而
,而![]() ,又易证当
,又易证当![]() 时,
时,![]() ,所以函数
,所以函数![]() 在
在![]() 内有一零点,故不满足条件.
内有一零点,故不满足条件.
综上可得:![]() 的取值范围为:
的取值范围为:![]() 或
或![]() .
.


 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案科目:高中数学 来源: 题型:
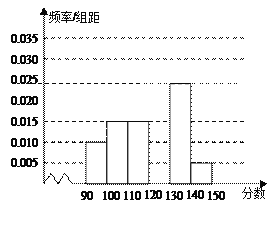
【题目】某校从参加高二某次月考的学生中随机抽取60名学生,将其数学成绩(均为整数)分成六组![]() 后得到如右所示的部分频率分布直方图。观察图形信息,回答下列问题:
后得到如右所示的部分频率分布直方图。观察图形信息,回答下列问题:
(Ⅰ)求分数在![]() 内的频率;
内的频率;
(Ⅱ)用分层抽样的方法在分数段![]() 的学生中抽取一个容量为6的样本,再从该样本中任取2人,求至多有1人在分数段
的学生中抽取一个容量为6的样本,再从该样本中任取2人,求至多有1人在分数段![]() 内的概率。
内的概率。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某手机卖场对市民进行国产手机认可度的调查,随机抽取100名市民,按年龄(单位:岁)进行统计的频数分布表和频率分布直方图如图:
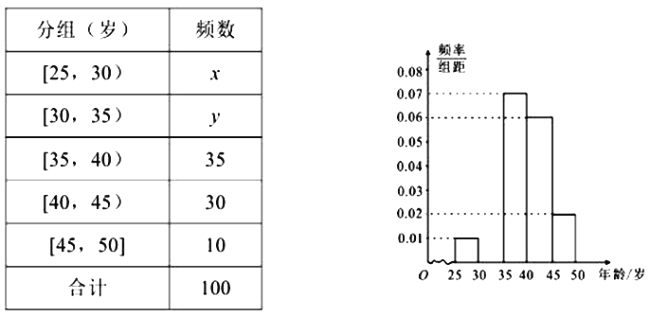
(Ⅰ)求频率分布表中![]() ,
,![]() 的值,并补全频率分布直方图;
的值,并补全频率分布直方图;
(Ⅱ)在抽取的这100名市民中,按年龄进行分层抽样,抽取20人参加国产手机用户体验问卷调查,现从这20人中随机选取2人各赠送精美礼品一份,设这2名市民中年龄在![]() 内的人数
内的人数![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,直线PQ与⊙O切于点A,AB是⊙O的弦,∠PAB的平分线AC交⊙O于点C,连接CB,并延长与直线PQ相交于Q点.
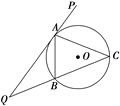
(1)求证:QC·AC=QC2-QA2;
(2)若AQ=6,AC=5,求弦AB的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
以直角坐标系![]() 的原点为极点,
的原点为极点, ![]() 轴的非负半轴为极轴建立极坐标系,且两坐标系有相同的长度单位.已知点
轴的非负半轴为极轴建立极坐标系,且两坐标系有相同的长度单位.已知点![]() 的极坐标为
的极坐标为![]() ,
, ![]() 是曲线
是曲线![]() :
: ![]() 上任意一点,点
上任意一点,点![]() 满足
满足![]() ,设点
,设点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(Ⅰ)求曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)若过点![]() 的直线
的直线![]() 的参数方程
的参数方程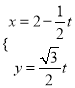 (
(![]() 为参数),且直线
为参数),且直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
, ![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知直线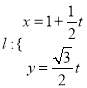 (
(![]() 为参数),曲线
为参数),曲线![]() (
(![]() 为参数).
为参数).
(1)设![]() 与
与![]() 相交于
相交于![]() 两点,求
两点,求![]() ;
;
(2)若把曲线![]() 上各点的横坐标压缩为原来的
上各点的横坐标压缩为原来的![]() 倍,纵坐标压缩为原来的
倍,纵坐标压缩为原来的![]() 倍,得到曲线
倍,得到曲线![]() ,设点
,设点![]() 是曲线
是曲线![]() 上的一个动点,求它到直线
上的一个动点,求它到直线![]() 的距离的最小值.
的距离的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校从高二年级学生中随机抽取60名学生,将其期中考试的政治成绩(均为整数)分成六段: ![]() ,
, ![]() ,
, ![]() ,…
,…![]() 后得到如下频率分布直方图.
后得到如下频率分布直方图.
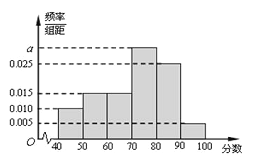
(1)根据频率分布直方图,估计该校高二年级学生期中考试政治成绩的中位数(精确到0.1)、众数、平均数;
(2)用分层抽样的方法抽取一个容量为20的样本,求各分数段抽取的人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com