
【题目】第7届世界军人运动会于2019年10月18日至27日在湖北武汉举行,赛期10天,共设置射击、游泳、田径、篮球等27个大项,329个小项.共有来自100多个国家的近万名现役军人同台竞技.前期为迎接军运会顺利召开,武汉市很多单位和部门都开展了丰富多彩的宣传和教育活动,努力让大家更多的了解军运会的相关知识,并倡议大家做文明公民.武汉市体育局为了解广大民众对军运会知识的知晓情况,在全市开展了网上问卷调查,民众参与度极高,现从大批参与者中随机抽取200名幸运参与者,他们得分(满分100分)数据,统计结果如下:
组别 |
|
|
|
|
|
|
|
频数 | 5 | 30 | 40 | 50 | 45 | 20 | 10 |
(1)若此次问卷调查得分整体服从正态分布,用样本来估计总体,设![]() ,
,![]() 分别为这200人得分的平均值和标准差(同一组数据用该区间中点值作为代表),求
分别为这200人得分的平均值和标准差(同一组数据用该区间中点值作为代表),求![]() ,
,![]() 的值(
的值(![]() ,
,![]() 的值四舍五入取整数),并计算
的值四舍五入取整数),并计算![]() ;
;
(2)在(1)的条件下,为感谢大家参与这次活动,市体育局还对参加问卷调查的幸运市民制定如下奖励方案:得分低于![]() 的可以获得1次抽奖机会,得分不低于
的可以获得1次抽奖机会,得分不低于![]() 的可获得2次抽奖机会,在一次抽奖中,抽中价值为15元的纪念品A的概率为
的可获得2次抽奖机会,在一次抽奖中,抽中价值为15元的纪念品A的概率为![]() ,抽中价值为30元的纪念品B的概率为
,抽中价值为30元的纪念品B的概率为![]() .现有市民张先生参加了此次问卷调查并成为幸运参与者,记Y为他参加活动获得纪念品的总价值,求Y的分布列和数学期望,并估算此次纪念品所需要的总金额.
.现有市民张先生参加了此次问卷调查并成为幸运参与者,记Y为他参加活动获得纪念品的总价值,求Y的分布列和数学期望,并估算此次纪念品所需要的总金额.
(参考数据:![]() ;
;![]() ;
;![]() .)
.)
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】新疆小南瓜以沙甜闻名全国,小田计划从新疆运输小南瓜去上海,随机从某瓜农的瓜地里挑选了100个,其质量分别在![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() (单位:克)中,经统计得频率分布直方图如图所示,将频率视为概率.
(单位:克)中,经统计得频率分布直方图如图所示,将频率视为概率.
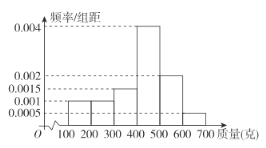
(1)请根据频率分布直方图估计该瓜农的小南瓜的平均质量;
(2)已知瓜地里还有2万个小南瓜已经成熟,可以采摘,小田想全部购买,可是瓜农要求超过400克的小南瓜以5元一个的价格出售,其他的以3元一个的价格出售.将频率视为概率,若新疆到上海往返的运费约2000元,请问这2万个小南瓜在上海以每斤(500克)多少元定价才能保证小田的利润不少于5000元?(结果保留一位小数)
(3)某天王阿姨在上海某超市的蔬菜柜台上看到小田从新疆采摘的新疆小南瓜,已知柜台上有若干个,若质量超过500克的小南瓜为“优质品”,王阿姨随机购买了20个小南瓜,求王阿姨购买的小南瓜中“优质品”个数的期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,随着我国汽车消费水平的提高,二手车流通行业得到迅猛发展.某汽车交易市场对2017年成交的二手车交易前的使用时间(以下简称“使用时间”)进行统计,得到频率分布直方图如图1.


图1 图2
(1)记“在![]() 年成交的二手车中随机选取一辆,该车的使用年限在
年成交的二手车中随机选取一辆,该车的使用年限在![]() ”为事件
”为事件![]() ,试估计
,试估计![]() 的概率;
的概率;
(2)根据该汽车交易市场的历史资料,得到散点图如图2,其中![]() (单位:年)表示二手车的使用时间,
(单位:年)表示二手车的使用时间,![]() (单位:万元)表示相应的二手车的平均交易价格.由散点图看出,可采用
(单位:万元)表示相应的二手车的平均交易价格.由散点图看出,可采用![]() 作为二手车平均交易价格
作为二手车平均交易价格![]() 关于其使用年限
关于其使用年限![]() 的回归方程,相关数据如下表(表中
的回归方程,相关数据如下表(表中![]() ,
,![]() ):
):

①根据回归方程类型及表中数据,建立![]() 关于
关于![]() 的回归方程;
的回归方程;
②该汽车交易市场对使用8年以内(含8年)的二手车收取成交价格![]() 的佣金,对使用时间8年以上(不含8年)的二手车收取成交价格
的佣金,对使用时间8年以上(不含8年)的二手车收取成交价格![]() 的佣金.在图1对使用时间的分组中,以各组的区间中点值代表该组的各个值.若以2017年的数据作为决策依据,计算该汽车交易市场对成交的每辆车收取的平均佣金.
的佣金.在图1对使用时间的分组中,以各组的区间中点值代表该组的各个值.若以2017年的数据作为决策依据,计算该汽车交易市场对成交的每辆车收取的平均佣金.
附注:①对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为 ;
;
②参考数据:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知平面向量![]() ,
,![]() 满足:|
满足:|![]() |=2,|
|=2,|![]() |=1.
|=1.
(1)若(![]() 2
2![]() )(
)(![]() )=1,求
)=1,求![]()
![]() 的值;
的值;
(2)设向量![]() ,
,![]() 的夹角为θ.若存在t∈R,使得
的夹角为θ.若存在t∈R,使得![]() ,求cosθ的取值范围.
,求cosθ的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“一带一路”是“丝绸之路经济带”和“21世纪海上丝绸之路”的简称,旨在积极发展我国与沿线国家经济合作关系,共同打造政治互信、经济融合、文化包容的命运共同体.自2015年以来,“一带一路”建设成果显著.如图是2015—2019年,我国对“一带一路”沿线国家进出口情况统计图,下列描述错误的是( )
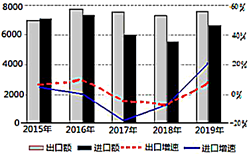
A.这五年,出口总额之和比进口总额之和大
B.这五年,2015年出口额最少
C.这五年,2019年进口增速最快
D.这五年,出口增速前四年逐年下降
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,分别过椭圆![]() 左、右焦点
左、右焦点![]() 的动直线
的动直线![]() 相交于
相交于![]() 点,与椭圆
点,与椭圆![]() 分别交于
分别交于![]() 与
与![]() 不同四点,直线
不同四点,直线![]() 的斜率
的斜率![]() 满足
满足![]() .已知当
.已知当![]() 与
与![]() 轴重合时,
轴重合时,![]() ,
,![]() .
.
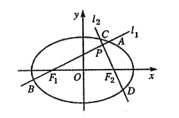
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)是否存在定点![]() ,使得
,使得![]() 为定值?若存在,求出
为定值?若存在,求出![]() 点坐标并求出此定值;若不存在,说明理由.
点坐标并求出此定值;若不存在,说明理由.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() ,
,![]() 和
和![]() .
.
【解析】试题分析:(1)当![]() 与
与![]() 轴重合时,
轴重合时,![]() 垂直于
垂直于![]() 轴,得
轴,得![]() ,得
,得![]() ,
,![]() 从而得椭圆的方程;(2)由题目分析如果存两定点,则
从而得椭圆的方程;(2)由题目分析如果存两定点,则![]() 点的轨迹是椭圆或者双曲线 ,所以把
点的轨迹是椭圆或者双曲线 ,所以把![]() 坐标化,可得
坐标化,可得![]() 点的轨迹是椭圆,从而求得定点
点的轨迹是椭圆,从而求得定点![]() 和点
和点![]() .
.
试题解析:![]() 当
当![]() 与
与![]() 轴重合时,
轴重合时,![]() , 即
, 即![]() ,所以
,所以![]() 垂直于
垂直于![]() 轴,得
轴,得![]() ,
,![]() ,, 得
,, 得![]() ,
,![]() 椭圆
椭圆![]() 的方程为
的方程为![]() .
.
![]() 焦点
焦点![]() 坐标分别为
坐标分别为![]() , 当直线
, 当直线![]() 或
或![]() 斜率不存在时,
斜率不存在时,![]() 点坐标为
点坐标为![]() 或
或![]() ;
;
当直线![]()
![]() 斜率存在时,设斜率分别为
斜率存在时,设斜率分别为![]() , 设
, 设![]()
![]() 由
由 , 得:
, 得:
![]() , 所以:
, 所以:![]() ,
,![]() , 则:
, 则:
![]()
![]() . 同理:
. 同理:![]()
![]() , 因为
, 因为
![]() , 所以
, 所以![]()
![]() , 即
, 即![]() , 由题意知
, 由题意知![]() , 所以
, 所以
![]() , 设
, 设![]() ,则
,则![]() ,即
,即![]() ,由当直线
,由当直线![]() 或
或![]() 斜率不存在时,
斜率不存在时,![]() 点坐标为
点坐标为![]() 或
或![]() 也满足此方程,所以点
也满足此方程,所以点![]() 在椭圆
在椭圆![]() 上.存在点
上.存在点![]() 和点
和点![]() ,使得
,使得![]() 为定值,定值为
为定值,定值为![]() .
.
考点:圆锥曲线的定义,性质,方程.
【方法点晴】本题是对圆锥曲线的综合应用进行考查,第一问通过两个特殊位置,得到基本量![]() ,
,![]() ,得
,得![]() ,
,![]() ,从而得椭圆的方程,第二问由题目分析如果存两定点,则
,从而得椭圆的方程,第二问由题目分析如果存两定点,则![]() 点的轨迹是椭圆或者双曲线 ,本题的关键是从这个角度出发,把
点的轨迹是椭圆或者双曲线 ,本题的关键是从这个角度出发,把![]() 坐标化,求得
坐标化,求得![]() 点的轨迹方程是椭圆
点的轨迹方程是椭圆![]() ,从而求得存在两定点
,从而求得存在两定点![]() 和点
和点![]() .
.
【题型】解答题
【结束】
21
【题目】已知![]() ,
,![]() ,
,![]() .
.
(Ⅰ)若![]() ,求
,求![]() 的极值;
的极值;
(Ⅱ)若函数![]() 的两个零点为
的两个零点为![]() ,记
,记![]() ,证明:
,证明:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我区的中小学办学条件在政府的教育督导下,迅速得到改变.督导一年后.分别随机抽查了高中(用![]() 表示)与初中(用
表示)与初中(用![]() 表示)各10所学校.得到相关指标的综合评价得分(百分制)的茎叶图如图所示.则从茎叶图可得出正确的信息为(80分及以上为优秀)( )
表示)各10所学校.得到相关指标的综合评价得分(百分制)的茎叶图如图所示.则从茎叶图可得出正确的信息为(80分及以上为优秀)( )
①高中得分与初中得分的优秀率相同
②高中得分与初中得分的中位数相同
③高中得分的方差比初中得分的方差大
④高中得分与初中得分的平均分相同
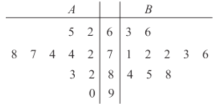
A.①②B.①③C.②④D.③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com