
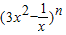 的展开式中各项系数的和是512,则展开式中的常数项为( )
的展开式中各项系数的和是512,则展开式中的常数项为( )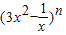 中,令x=1可得,其展开式各项系数的和,又由题意,可得2n=512,解可得n=9,进而可得其展开式的通项,在其中令x的指数为0,可得r的值为6,即可得其展开式中的常数项,即可得答案.
中,令x=1可得,其展开式各项系数的和,又由题意,可得2n=512,解可得n=9,进而可得其展开式的通项,在其中令x的指数为0,可得r的值为6,即可得其展开式中的常数项,即可得答案.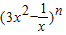 中,令x=1可得,其展开式各项系数的和是2n,
中,令x=1可得,其展开式各项系数的和是2n,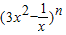 的展开式的通项为Tr+1=C9r(3x2)9-r(-
的展开式的通项为Tr+1=C9r(3x2)9-r(- )r=(-1)r•C9r•39-rx18-3r,
)r=(-1)r•C9r•39-rx18-3r,

科目:高中数学 来源:2011年福建省高二上学期期末考试数学理卷 题型:选择题
为落实素质教育,某中学拟从4个重点研究性课题和6个一般研究性课题中各选2个课题作为本年度该校启动的课题项目,若重点研究性课题A和一般研究性课题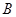 中至少有一个被选中的不同选法种数是
中至少有一个被选中的不同选法种数是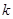 ,那么二项式
,那么二项式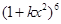 的展开式中
的展开式中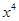 的系数为
的系数为
A.50000 B.54000 C.56000 D.59000
查看答案和解析>>
科目:高中数学 来源: 题型:
为落实素质教育,某中学拟从4个重点研究性课题和6个一般研究性课题中各选2个课题作为本年度该校启动的课题项目,若重点研究性课题A和一般研究性课题![]() 中至少有一个被选中的不同选法种数是
中至少有一个被选中的不同选法种数是![]() ,那么二项式
,那么二项式![]() 的展开式中
的展开式中![]() 的系数为
的系数为
A.50000 B.54000 C.56000 D.59000
查看答案和解析>>
科目:高中数学 来源: 题型:
为落实素质教育,某中学拟从4个重点研究性课题和6个一般研究性课题中各选2个课题作为本年度该校启动的课题项目,若重点研究性课题A和一般研究性课题![]() 中至少有一个被选中的不同选法种数是
中至少有一个被选中的不同选法种数是![]() ,那么二项式
,那么二项式![]() 的展开式中
的展开式中![]() 的系数为
的系数为
A.50000 B.54000 C.56000 D.59000
查看答案和解析>>
科目:高中数学 来源:安徽省08-09学年高二下学期六校联考(理) 题型:选择题
为落实素质教育,某中学拟从4个重点研究性课题和6个一般研究性课题中各选2个课题作为本年度该校启动的课题项目,若重点研究性课题A和一般研究性课题 中至少有一个被选中的不同选法种数是
中至少有一个被选中的不同选法种数是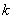 ,那么二项式
,那么二项式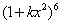 的展开式中
的展开式中 的系数为
的系数为
A.50000 B.54000 C.56000 D.59000
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com