
分析 (1)根据条件求出注水量和泄水量,即可得到结论.
(2)根据堤坝会发生危险的条件,解不等式即可.
解答 解:(1)设第n天注入水库的水量为5000$\sqrt{n(n+24)}$立方米,泄水为4000n立方米,
则第n天水库的容水量为f(n)=8000+5000$\sqrt{n(n+24)}$-4000n,(n∈N+,n≤10).
(2)设第n天会发生危险,则
5000$\sqrt{n(n+24)}$-4000n≥128000-80000,
即5$\sqrt{n(n+24)}$≥4n+48,
也即n2+24n-256≥0,
解得n≤-32或n≥8,
由于n∈N,所以取n≥8,即第8天时,总水量就超过水库的最大容量,也即该水库堤坝在第8天会发生危险.
点评 本题主要考查函数的应用问题,根据条件建立函数关系是解决本题的关键.


科目:高中数学 来源: 题型:选择题
| A. | (0,1) | B. | (0,$\frac{1}{2}$) | C. | (-∞,2) | D. | (-∞,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
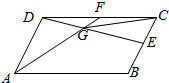 如图,已知E,F分别是平行四边形ABCD的边BC,CD中点,AF与DE相交于点G,若$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$,则$\overrightarrow{GC}$=$\frac{3}{5}\overrightarrow{a}+\frac{1}{5}\overrightarrow{b}$(用$\overrightarrow{a}$,$\overrightarrow{b}$表示)
如图,已知E,F分别是平行四边形ABCD的边BC,CD中点,AF与DE相交于点G,若$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$,则$\overrightarrow{GC}$=$\frac{3}{5}\overrightarrow{a}+\frac{1}{5}\overrightarrow{b}$(用$\overrightarrow{a}$,$\overrightarrow{b}$表示)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{4}$ | B. | -$\frac{7}{4}$ | C. | -$\frac{5}{4}$ | D. | -$\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{π}{6}$] | B. | (0,$\frac{π}{3}$] | C. | (0,$\frac{π}{2}$] | D. | [$\frac{π}{3}$,$\frac{2π}{3}$] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com