练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    某城市要建成宜商、宜居的国际化现代新城，该城市的东城区、西城区分别引进8甲厂家，现对两个区域的16个厂家进行评估，综合得分情况如茎叶图所示.

    （1）根据茎叶图判断哪个区域厂家的平均分较高；
    （2）规定85分以上（含85分）为优秀厂家，若从该两个区域各选一个优秀厂家，求得分差距不超过5分的概率.

    （1）东城区的平均分较高.（2）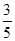

    解析试题分析：（1）根据茎叶图的含义，分别写出东城区和西城区16个厂家进行评估得分，然后在计算平均分；
    （2）两个区域各选一个优秀厂家，所有的基本事件共15种，然后找出分差距不超过5的事件并计算出基本事件个数，最后根据随机事件的概率公式求解.

    试题解析：（1）东城区的平均分较高.（结论正确即给分）        5分
    （2）从两个区域各选一个优秀厂家，
    则所有的基本事件共15种，      7分
    满足得分差距不超过5的事件（88,85）（88,85）（89,85）（89,94）（89,94）（93，94）（93，94）（94,,94）（94,,94）共9种.     10分
    所以满足条件的概率为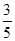.      12分
    考点：1.根据样本估计总体；2.随机事件的概率.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    （13分）（2011•天津）编号为A1，A2，…，A16的16名篮球运动员在某次训练比赛中的得分记录如下：

    运动员编号
    		A1
    		A2
    		A3
    		A4
    		A5
    		A6
    		A7
    		A8
    		 
     
    		得分
    		15
    		35
    		21
    		28
    		25
    		36
    		18
    		34
    运动员编号
    		A9
    		A10
    		A11
    		A12
    		A13
    		A14
    		A15
    		A16
    		 
     
    		得分
    		17
    		26
    		25
    		33
    		22
    		12
    		31
    		38
    （Ⅰ）将得分在对应区间内的人数填入相应的空格；
    区间
    		[10，20）
    		[20，30）
    		[30，40]
    人数
    		 
    		 
    		 
    （Ⅱ）从得分在区间[20，30）内的运动员中随机抽取2人，
    （i）用运动员的编号列出所有可能的抽取结果；
    （ii）求这2人得分之和大于50分的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    有7位歌手(1至7号)参加一场歌唱比赛, 由500名大众评委现场投票决定歌手名次, 根据年龄将大众评委分为5组, 各组的人数如下:

    组别
    		A
    		B
    		C
    		D
    		E
    人数
    		50
    		100
    		150
    		150
    		50
     
    （1）为了调查评委对7位歌手的支持状况, 现用分层抽样方法从各组中抽取若干评委, 其中从B组中抽取了6人. 请将其余各组抽取的人数填入下表.
    组别
    		A
    		B
    		C
    		D
    		E
    人数
    		50
    		100
    		150
    		150
    		50
    抽取人数
    		 
    		6
    		 
    		 
    		 
     
    （2）在（1）中, 若A, B两组被抽到的评委中各有2人支持1号歌手, 现从这两组被抽到的评委中分别任选1人, 求这2人都支持1号歌手的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    某公司生产产品A，产品质量按测试指标分为：指标大于或等于90为一等品，大于或等于小于为二等品，小于为三等品，生产一件一等品可盈利50元，生产一件二等品可盈利元，生产一件三等品亏损10元．现随机抽查熟练工人甲和新工人乙生产的这种产品各100件进行检测，检测结果统计如下：

    测试指标






    甲
    		3
    		7
    		20
    		40
    		20
    		10
    乙
    		5
    		15
    		35
    		35
    		7
    		3
     
    现将根据上表统计得到甲、乙两人生产产品A为一等品、二等品、三等品的频率分别估计为他们生产产品A为一等品、二等品、三等品的概率．
    （1）计算新工人乙生产三件产品A，给工厂带来盈利大于或等于100元的概率；
    （2）记甲乙分别生产一件产品A给工厂带来的盈利和记为X，求随机变量X的概率分布和数学期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    为了调查某厂2000名工人生产某种产品的能力，随机抽查了位工人某天生产该产品的数量，产品数量的分组区间为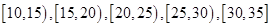，得到如题（16）图所示的频率分布直方图。已知生产的产品数量在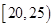之间的工人有6位.
    （1）求；
    （2）工厂规定从生产低于20件产品的工人中随机的选取2位工人进行培训，求这2位工人不在同一组的概率.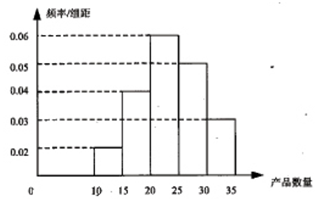

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    小明家订了一份报纸，寒假期间他收集了每天报纸送达时间的数据，并绘制成频率分布直方图，如图所示．

    （1）根据图中的数据信息，写出众数；
    （2）小明的父亲上班离家的时间在上午之间，而送报人每天在时刻前后
    半小时内把报纸送达（每个时间点送达的可能性相等）．
    ①求小明的父亲在上班离家前能收到报纸（称为事件）的概率；
    ②求小明的父亲周一至周五在上班离家前能收到报纸的天数的数学期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    在电阻碳含量对于电阻的效应研究中，得到如下表所示的数据：

    含碳量
    (x/%)
    		0.10
    		0.30
    		0.40
    		0.55
    		0.70
    		0.80
    		0.95
    20 ℃时电阻
    (y/Ω)
    		15
    		18
    		19
    		21
    		22.6
    		23.8
    		26
    (1)求出y与x的相关系数并判断相关性；
    (2)求出电阻y关于含碳量x之间的回归直线方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    年龄在60岁（含60岁）以上的人称为老龄人，某小区的老龄人有350人，他们的健康状况如下表：

    其中健康指数的含义是：2代表“健康”，1代表“基本健康”，0代表“不健康，但生活能够自理”，-1代表“生活不能自理”。
    （1）随机访问该小区一位80岁以下的老龄人，该老人生活能够自理的概率是多少？
    （2）按健康指数大于0和不大于0进行分层抽样，从该小区的老龄人中抽取5位，并随机地访问其中的3位.求被访问的3位老龄人中恰有1位老龄人的健康指数不大于0的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    已知一组数据的频率分布直方图如下.求众数、中位数、平均数.

    查看答案和解析>>

    同步练习册答案