
【题目】求经过三点A(1,4),B(﹣2,3),C(4,﹣5)的圆的方程.
【答案】解:设经过三点A(1,4),B(﹣2,3),C(4,﹣5)的圆的方程为x2+y2+Dx+Ey+F=0, ∵点A(1,4),B(﹣2,3),C(4,﹣5)三点在圆上,
∴将A、B、C的坐标代入,
可得 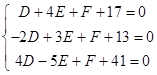 ,
,
解得 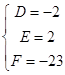 ,故圆的方程为x2+y2 ﹣2x+2y﹣23=0
,故圆的方程为x2+y2 ﹣2x+2y﹣23=0
【解析】设圆的方程为x2+y2+Dx+Ey+F=0,将A、B、C的坐标代入得到关于D、E、F的方程组,解之得到圆的方程.
【考点精析】根据题目的已知条件,利用圆的一般方程的相关知识可以得到问题的答案,需要掌握圆的一般方程的特点:(1)①x2和y2的系数相同,不等于0.②没有xy这样的二次项;(2)圆的一般方程中有三个特定的系数D、E、F,因之只要求出这三个系数,圆的方程就确定了;(3)、与圆的标准方程相比较,它是一种特殊的二元二次方程,代数特征明显,圆的标准方程则指出了圆心坐标与半径大小,几何特征较明显.


科目:高中数学 来源: 题型:
【题目】△ABC的三个内角A、B、C的对边分别是a,b,c,给出下列命题: ①若sinBcosC>﹣cosBsinC,则△ABC一定是钝角三角形;
②若sin2A+sin2B=sin2C,则△ABC一定是直角三角形;
③若bcosA=acosB,则△ABC为等腰三角形;
④在△ABC中,若A>B,则sinA>sinB;
其中正确命题的序号是 . (注:把你认为正确的命题的序号都填上)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}的前n项和为Sn , S3=15,a3和a5的等差中项为9
(1)求an及Sn
(2)令bn= ![]() (n∈N*),求数列{bn}的前n项和Tn .
(n∈N*),求数列{bn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,若圆C的圆心在第一象限,圆C与x轴相交于A(1,0)、B(3,0)两点,且与直线x﹣y+1=0相切,则圆C的标准方程为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,点A(1,1),B(0,﹣2),C(4,2),D为AB的中点,DE∥BC. (Ⅰ)求BC边上的高所在直线的方程;
(Ⅱ)求DE所在直线的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
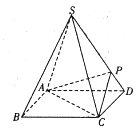
【题目】如图,四棱锥![]() 的底面是正方形,每条侧棱的长都是底面边长的
的底面是正方形,每条侧棱的长都是底面边长的![]() 倍,P为侧棱SD上的点,且
倍,P为侧棱SD上的点,且![]() .
.
(1)求二面角![]() 的大小;
的大小;
(2)在侧棱SC上是否存在一点E,使得![]() 平面
平面![]() ?若存在,求
?若存在,求![]() 的值;若不存在,试说明理由.
的值;若不存在,试说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的一个焦点与
的一个焦点与![]() 的焦点重合,点
的焦点重合,点![]() 在椭圆
在椭圆![]() 上.
上.
(1)求椭圆![]() 的方程;
的方程;
(2)设直线![]() :
: ![]() (
(![]() )与椭圆
)与椭圆![]() 交于
交于![]() 两点,且以
两点,且以![]() 为对角线的菱形的一顶点为
为对角线的菱形的一顶点为![]() ,求
,求![]() 面积的最大值(
面积的最大值(![]() 为坐标原点).
为坐标原点).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某次测试后,一位老师从本班48同学中随机抽取6位同学,他们的语文、历史成绩如下表:
学生编号 | 1 | 2 | 3 | 4 | 5 | 6 |
语文成绩 | 60 | 70 | 74 | 90 | 94 | 110 |
历史成绩 | 58 | 63 | 75 | 79 | 81 | 88 |
(1)若规定语文成绩不低于90分为优秀,历史成绩不低于80分为优秀,以频率作概率,分别估计该班语文、历史成绩优秀的人数;
(2)用上表数据画出散点图易发现历史成绩![]() 与语文成绩
与语文成绩![]() 具有较强的线性相关关系,求
具有较强的线性相关关系,求![]() 与
与![]() 的线性回归方程(系数精确到0.1).
的线性回归方程(系数精确到0.1).
参考公式:回归直线方程是![]() ,其中
,其中![]() ,
, ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com