
����Ŀ����ͼ1��ʾΪһ��ħ�����ƣ�ͼ2Ϊ�õ��ƵĿ�ܽṹͼ����������![]() ��
��![]() ���ɣ��������IJ��ⳤ����ȣ������������Բ��ֱ��Ϊ
���ɣ��������IJ��ⳤ����ȣ������������Բ��ֱ��Ϊ![]() ����������Ϊ
����������Ϊ![]() ��ͨ�����������̶̹����컨���ϣ�ʹ���ĵ����ˮƽ״̬���¶���
��ͨ�����������̶̹����컨���ϣ�ʹ���ĵ����ˮƽ״̬���¶���![]() ���컨��ľ���Ϊ
���컨��ľ���Ϊ![]() �����е������߶�������Ľ������Ƴɣ�����������ܳ�Ϊy��
�����е������߶�������Ľ������Ƴɣ�����������ܳ�Ϊy��
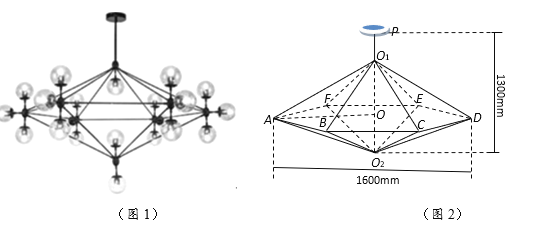
��1�����O1AO =![]() (rad)����y��ʾ�����ĺ�����ϵʽ����д�����ķ�Χ��
(rad)����y��ʾ�����ĺ�����ϵʽ����д�����ķ�Χ��![]()
��2�����������������������ֵ�Ĵ�С�Ƕ���ʱ���������ܳ�y��С��
���𰸡���1��![]() ��
��![]() ��
��![]() ��
��![]() ������2������
������2������![]() ����
����![]() ��
��![]() ��ʱ���������ܳ�y��С��
��ʱ���������ܳ�y��С��
��������
��1����ֱ��������OAO1�У��������Ǻ����Ķ��壬��![]() ��ʾ
��ʾ![]() ��������ʵ������ɵ����ķ�Χ�����ѵ���12�����⣬6���ױߣ�1����������ӱ�ʾy���ô𰸣�
��������ʵ������ɵ����ķ�Χ�����ѵ���12�����⣬6���ױߣ�1����������ӱ�ʾy���ô𰸣�
��2��Ϊ�˷������㣬ֻ��![]() �������ķ�ʽ�ü�ֵ����ʱ��Ϊ��Сֵ.
�������ķ�ʽ�ü�ֵ����ʱ��Ϊ��Сֵ.
��1����ֱ��������OAO1�У�![]() ��
��![]() ��
��
��![]() ������
������![]() ��
��
�������ķ�Χ��![]() ������
������![]() ��
��![]() ��
��
�Ӷ���![]()
![]()
![]() ��
��
����![]() ��
��![]() ��
��![]() ��
��![]() ����
����
��2����![]() ������
������![]() ��
��
��![]() ����
����![]() ����
����![]() ��
��
��![]() ʱ��
ʱ��![]() ����
����![]() ʱ��
ʱ��![]() ��
��
����![]() �ĵ�������
�ĵ�������![]() ��ϵ�б����£�
��ϵ�б����£�
|
|
|
|
|
| 0 | + |
|
| ��Сֵ |
|
���Ե�![]() ������
������![]() ʱ
ʱ![]() ȡ����Сֵ����y��С��
ȡ����Сֵ����y��С��
�ʵ���![]() ����
����![]() ��
��![]() ��ʱ���������ܳ�y��С��
��ʱ���������ܳ�y��С��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������![]() �IJ���͵���߳���ȣ��������������
�IJ���͵���߳���ȣ��������������![]() ��������ȡ�����������з�ʽ�����������
��������ȡ�����������з�ʽ�����������![]() ��ֵ��
��ֵ��
�������������ڵ�ֱ���ཻ����![]() ��ֵ��������������ֱ�ߵļнǴ�С�������ƣ���
��ֵ��������������ֱ�ߵļнǴ�С�������ƣ���
�������������ڵ�ֱ��ƽ�У���![]() ��
��
�������������ڵ�ֱ�����棬��![]() ��ֵ��������������ֱ�����ɽǵĴ�С(������).
��ֵ��������������ֱ�����ɽǵĴ�С(������).
��1����![]() ��ֵ��
��ֵ��
��2�����������![]() �ķֲ��м���ѧ����
�ķֲ��м���ѧ����![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
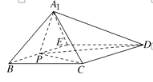
����Ŀ����ͼ�����ı���ABCD�У�AD��BC����BAD��90����AB��2![]() ��BC��4��AD��6��E��AD�ϵĵ㣬AE��
��BC��4��AD��6��E��AD�ϵĵ㣬AE��![]() AD��P ΪBE���е㣬����ABE��BE������A1BE��λ�ã�ʹ��A1C��4����ͼ��ʾ.������BA1PD������ֵ��
AD��P ΪBE���е㣬����ABE��BE������A1BE��λ�ã�ʹ��A1C��4����ͼ��ʾ.������BA1PD������ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪a��0������f��x����|2x+2|+|x��a|����СֵΪ2��

��1����ʵ��a��ֵ��������y��f��x����ͼ��
��2����m��0��n��0����m+n��2![]() ʱ��m2+n2��f��x�����������ʵ��x��ȡֵ��Χ��
ʱ��m2+n2��f��x�����������ʵ��x��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��B,C�ֱ��Ǻ������ϵ����������������м��ɱ�ֱ�ĺ�����·������B��C֮��ľ���Ϊ100km������A�ڳ���B��������50![]() �����Ӻ���A������C���ȳ˴�����ƫ�����ǣ�
�����Ӻ���A������C���ȳ˴�����ƫ�����ǣ�![]() ���������
���������![]() ������ֵΪ
������ֵΪ![]() �����е�������·P����½���ٻ�������������C����֪����Ϊ25km/h������Ϊ75km/h.
�����е�������·P����½���ٻ�������������C����֪����Ϊ25km/h������Ϊ75km/h.
��1���Խ�����A��P��C����ʱ����![]() �ĺ�������ʽ��
�ĺ�������ʽ��
��2����ȷ����½��P��λ�ã�ʹ����ʱ�����٣���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ij��ɽ����ɽ��![]() �����ɽ��
�����ɽ��![]() ������Ϊ
������Ϊ![]() ������б��Ϊ
������б��Ϊ![]() ������
������![]() ����б��ǰ��
����б��ǰ��![]() ��
��![]() ������Ϣ�������ʻ
������Ϣ�������ʻ![]() ����ɽ��
����ɽ��![]() ��
��

��1����ɽ�ĸ߶�![]() ��
��
��2����ɽ������һ��![]() ����
����![]() ��
��![]() �ĵ�ɽ;�У���Ա�ڵ�
�ĵ�ɽ;�У���Ա�ڵ�![]() ����������ӽ�Ϊ
����������ӽ�Ϊ![]() ������
������![]() ���߶�
���߶�![]() Ϊ
Ϊ![]() ����
����![]() Ϊ��ֵʱ���ӽ�
Ϊ��ֵʱ���ӽ�![]() ���
���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2019��7��1��ӭ�����ҹ�����98���꣬6���ϵ�Ա��������Լ��������ʥ��֮һ��������.6���ϵ�Ա����3����Ա������ͬһ���࣬����վ��һ����������ʱ��Ҫ��ͬ���3����Ավ��һ��������������ÿ���ŷ���Ҫ��һ����Ƭ��������Ƭϴ������ÿ����Ƭ0.5Ԫ���������ܷѣ�������һ�����Ƭ��Ҫ���ܣ�ÿ�Ź��ܷ�Ϊ0.75Ԫ.������Щ��Ƭƽ���ָ�ÿ���ϵ�Ա�����ܵ���ƬҲҪƽ���֣�����ÿ���ϵ�Ա��Ҫ֧������Ƭ��Ϊ�� ��
A.20.5B.21ԪC.21.5ԪD.22Ԫ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxoy�У�������ԭ��OΪ���㣬x��������Ϊ���Ὠ��������ϵ����֪����C�ļ����귽��Ϊ![]() ������
������![]() ��ֱ��l�IJ�������Ϊ
��ֱ��l�IJ�������Ϊ ��Ϊ��������ֱ��l������C����M��N���㡣
��Ϊ��������ֱ��l������C����M��N���㡣
��1��д��ֱ��l����ͨ���̺�����C��ֱ�����귽�̣�
��2����![]() �ɵȱ����У���a��ֵ��
�ɵȱ����У���a��ֵ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com