
分析 (Ⅰ)求导,利用导数几何意义,导数与切线斜率的关系,联立方程即可求得b=$\frac{1}{2}$,c=$\frac{1}{2}$-a,对任意x∈R,都有x≤f'(x)恒成立,转化成ax2-$\frac{1}{2}$x+$\frac{1}{2}$-a≥0恒成立,则$\left\{\begin{array}{l}{a>0}\\{△<0}\end{array}\right.$,即可求得a和c的值,求得f(x)的解析式;
(Ⅱ)由(Ⅰ)可知,求得g(x),求导,利用二次函数的性质即可求得在$[{\frac{1}{2},2}]$上的最大值;
(Ⅲ)由题意可知m≥[x-x2lnx]max,构造函数,求导,根据函数的单调性即可求得函数的最大值,即可求得m的取值范围.
解答 解:(Ⅰ)∵求导f(x)=$\frac{1}{3}$ax3+$\frac{1}{2}$bx2+cx,f′(x)=ax2+bx+c,
因为函数f(x)的图象在点(-1,f(-1))处的切线与x轴平行,
∴f′(-1)=0,即a-b+c=0,①,
而f′(1)=1,即a+b+c=1,②,
由①②可解得b=$\frac{1}{2}$,c=$\frac{1}{2}$-a,
由对任意x∈R,x∈R,都有x≤f'(x)恒成立.
即ax2-$\frac{1}{2}$x+$\frac{1}{2}$-a≥0恒成立.则$\left\{\begin{array}{l}{a>0}\\{△<0}\end{array}\right.$,即$\left\{\begin{array}{l}{a>0}\\{16{a}^{2}-8a+1≤0}\end{array}\right.$,
解得:a=$\frac{1}{4}$.
∴f(x)=$\frac{1}{12}$x3+$\frac{1}{4}$x2+$\frac{1}{4}$x;
(II)∵g(x)=12f(x)-4x2-3x-3=x3+4x2+3x-4x2-3x-3=x3-x2-3,
∴求导,g′(x)=3x2-2x=x(3x-2),
当x∈[$\frac{1}{2}$,$\frac{2}{3}$]时,g′(x)<0,此时函数g(x)单调递减,
此时g(x)max=g($\frac{1}{2}$)=-$\frac{25}{8}$;
当x∈[$\frac{2}{3}$,2]时,g′(x)>0,此时函数g(x)单调递增,此时g(x)max=g(2)=1;
因为g(2)>g($\frac{1}{2}$),当x∈[$\frac{2}{3}$,2]时,g(x)max=g(2)=1;
∴g(x)在$[{\frac{1}{2},2}]$上的最大值1;
( III)∵h(x)=$\frac{m}{x}$+x•lnx,对任意x1,x2∈$[{\frac{1}{2},2}]$,都有h(x1)≥g(x2),则x∈[$\frac{2}{3}$,2]时,都有h(x)≥g(x)max=1,
∴m≥x-x2lnx,则m≥[x-x2lnx]max.令p(x)=x-x2lnx,$\frac{1}{2}$≤x≤2,
∴p′(x)=1-2xlnx-x,
则p′(x)=0,当x∈(1,2)时,p′(x)=1-x-2xlnx<-2xlnx<0,
此时p(x)单调递减;
当x∈($\frac{1}{2}$,1)时,p′(x)=1-x-2xlnx>-2xlnx>0,
此时p(x)单调递增,
∴p(x)max=p(1)=1,
∴m≥1,
实数m的取值范围[1,+∞).
点评 本题考查导数的综合应用,导数与函数单调性的关系,利用导数求函数的最值,二次函数的性质,考查转化思想,属于中档题.


 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {0,1} | B. | {-1,0,1,2} | C. | {0,1,2} | D. | {-1,0,1} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 支持希拉里 | 支持特朗普 | 合计 | |
| 男员工 | |||
| 女员工 | |||
| 合计 |
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| K0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
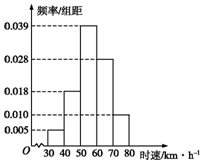 某时段内共有100辆汽车经过某一雷达地区,汽车时速的频率分布直方图如图所示,则时速不低于60km/h的汽车数量为( )
某时段内共有100辆汽车经过某一雷达地区,汽车时速的频率分布直方图如图所示,则时速不低于60km/h的汽车数量为( )| A. | 38 | B. | 28 | C. | 10 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com