
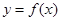
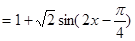 .
.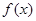 的最小正周期和最大值;
的最小正周期和最大值;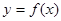 在区间
在区间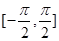 上的图象.
上的图象.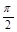 ,且方程
,且方程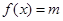 有两个不同的实数根,求实数m的取值范围.
有两个不同的实数根,求实数m的取值范围.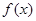 的最小正周期为
的最小正周期为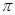 ,最大值为
,最大值为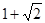 .
.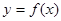 在区间
在区间 上的图象是
上的图象是
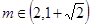 .
.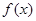 的最大值为
的最大值为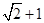 。
。 内有两个不同的实数根,
内有两个不同的实数根,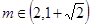 .
.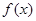 的最小正周期为
的最小正周期为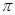 ,最大值为
,最大值为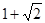 .
.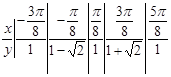
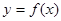 在区间
在区间 上的图象是
上的图象是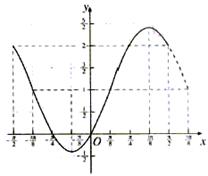
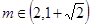 .
.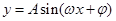 的图像及性质,五点法作图.
的图像及性质,五点法作图.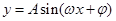 的图像及性质是解决此类问题的关键,其周期
的图像及性质是解决此类问题的关键,其周期 ,单调区间借助正弦函数的单调区间建立关于x的不等式求出解集即可。图像要利用五点法作图。
,单调区间借助正弦函数的单调区间建立关于x的不等式求出解集即可。图像要利用五点法作图。

 名校课堂系列答案
名校课堂系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com