
【题目】甲、乙两个篮球运动员互不影响地在同一位置投球,命中率分别为![]() 与
与![]() ,且乙投球3次均未命中的概率为
,且乙投球3次均未命中的概率为![]() ,甲投球未命中的概率恰是乙投球未命中的概率的2倍.
,甲投球未命中的概率恰是乙投球未命中的概率的2倍.
(Ⅰ)求乙投球的命中率![]() ;
;
(Ⅱ)若甲投球1次,乙投球2次,两人共命中的次数记为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】.如图,在三棱锥V-ABC中,VO⊥平面ABC,O∈CD,VA=VB,AD=BD,则下列结论中不一定成立的是 ( )
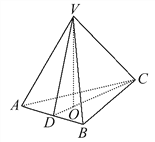
A. AC=BC
B. VC⊥VD
C. AB⊥VC
D. S△VCD·AB=S△ABC·VO
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知e为自然对数的底数,设函数![]() ,则( ).
,则( ).
A. 当k=1时,f(x)在x=1处取到极小值 B. 当k=1时,f(x)在x=1处取到极大值
C. 当k=2时,f(x)在x=1处取到极小值 D. 当k=2时,f(x)在x=1处取到极大值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小五、小一、小节、小快、小乐五位同学站成一排,若小一不出现在首位和末位,小五、小节、小乐中有且仅有两人相邻,求能满足条件的不同排法共有多少种?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,横、纵坐标均为整数的点叫做格点.若函数图象恰好经过k个格点,则称函数为k阶格点函数.已知函数:
①y=sinx; ②y=cos(x+![]() ); ③y=ex-1; ④y=x2.
); ③y=ex-1; ④y=x2.
其中为一阶格点函数的序号为 ( )
A. ①② B. ②③ C. ①③ D. ②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】16艘轮船的研究中,船的吨位区间为[192,3 246](单位:吨),船员的人数5~32人,船员人数y关于吨位x的回归方程为![]() =9.5+0.006 2x,
=9.5+0.006 2x,
(1)若两艘船的吨位相差1 000,求船员平均相差的人数.
(2)估计吨位最大的船和最小的船的船员人数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线C1![]() (t为参数),C2
(t为参数),C2 ![]() (θ为参数),
(θ为参数),
(Ⅰ)当α=![]() 时,求C1与C2的交点坐标;
时,求C1与C2的交点坐标;
(Ⅱ)过坐标原点O做C1的垂线,垂足为A,P为OA中点,当α变化时,求P点的轨迹的参数方程,并指出它是什么曲线.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】经市场调查,某商品在过去的20天内的价格![]() (单位:元)与销售量
(单位:元)与销售量![]() (单位:件)均为时间
(单位:件)均为时间![]() (单位:天)的函数,且价格满足
(单位:天)的函数,且价格满足![]() ,销售量满足
,销售量满足![]() ,其中
,其中![]() ,
, ![]() .
.
(1)请写出该商品的日销售额![]() (单位:元)与时间
(单位:元)与时间![]() (单位:天)的函数解析式;
(单位:天)的函数解析式;
(2)求该商品的日销售额的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com