
【题目】如图,在多面体ABCDPE中,四边形ABCD和CDPE都是直角梯形,AB∥DC,PE∥DC,AD⊥DC,PD⊥平面ABCD,AB=PD=DA=2PE,CD=3PE,F是CE的中点. 
(1)求证:BF∥平面ADP;
(2)求二面角B﹣DF﹣P的余弦值.
【答案】
(1)证明:取PD中点G,连结GF,AG,
∵AB∥DC,PE∥DC,AD⊥DC,PD⊥平面ABCD,AB=PD=DA=2PE,CD=3PE,F是CE的中点,
∴FG ![]() AB,∴四边形ABFG是平行四边形,∴AG∥BF,
AB,∴四边形ABFG是平行四边形,∴AG∥BF,
∵AG平面ADP,BF平面ADP,∴BF∥平面ADP
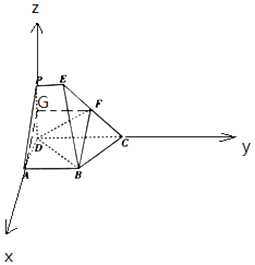
(2)解:以D为原点,DA为x轴,DC为y轴,DP为z轴,建立空间直角坐标系,
设PE=1,则B(2,2,0),D(0,0,0),P(0,0,2),C(0,3,0),E(0,1,2),F(0,2,1),
![]() =(2,2,0),
=(2,2,0), ![]() =(0,2,1),
=(0,2,1), ![]() =(0,0,2),
=(0,0,2),
设平面BDF的法向量 ![]() =(x,y,z),
=(x,y,z),
则  ,取x=1,得
,取x=1,得 ![]() =(1,﹣1,2),
=(1,﹣1,2),
设平面PDF的法向量 ![]() =(a,b,c),
=(a,b,c),
则 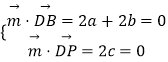 ,取a=1,则
,取a=1,则 ![]() =(1,﹣1,0),
=(1,﹣1,0),
设二面角B﹣DF﹣P的平面角为θ,
则cosθ= ![]() =
= ![]() =
= ![]() .
.
∴二面角B﹣DF﹣P的余弦值为 ![]() .
.
【解析】(1)取PD中点G,连结GF,AG,推导出四边形ABFG是平行四边形,从而AG∥BF,进而能证明BF∥平面ADP.(2)以D为原点,DA为x轴,DC为y轴,DP为z轴,建立空间直角坐标系,利用向量法能求出二面角B﹣DF﹣P的余弦值.
【考点精析】掌握直线与平面平行的判定是解答本题的根本,需要知道平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行.


科目:高中数学 来源: 题型:
【题目】某中学随机选取了40名男生,将他们的身高作为样本进行统计,得到如图所示的频率分布直方图.观察图中数据,完成下列问题. 
(Ⅰ)求a的值及样本中男生身高在[185,195](单位:cm)的人数;
(Ⅱ)假设同一组中的每个数据可用该组区间的中点值代替,通过样本估计该校全体男生的平均身高;
(Ⅲ)在样本中,从身高在[145,155)和[185,195](单位:cm)内的男生中任选两人,求这两人的身高都不低于185cm的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三行三列的方阵中有9个数aij(i=1,2,3;j=1,2,3),从中任取三个数,则至少有两个数位于同行或同列的概率是( ) 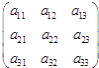
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=|x﹣a|,a∈R.
(1)当a=1时,求不等式f(x)+|2x﹣5|≥6的解集;
(2)若函数g(x)=f(x)﹣|x﹣3|的值域为A,且[﹣1,2]A,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】春节期间商场为活跃节日气氛,特举行“购物有奖”抽奖活动,举办方设置了甲、乙两种抽奖方案,方案甲的中奖率为 ![]() ,每次中奖可以获得20元购物代金券,方案乙的中奖率为
,每次中奖可以获得20元购物代金券,方案乙的中奖率为 ![]() ,每次中奖可以获得30元购物代金券,未中奖则不获得购物代金券,每次抽奖中奖与否互不影响,已知小明通过购物获得了2次抽奖机会.
,每次中奖可以获得30元购物代金券,未中奖则不获得购物代金券,每次抽奖中奖与否互不影响,已知小明通过购物获得了2次抽奖机会.
(1)若小明选择方案甲、乙各抽奖一次,记他累计获得的购物代金券面额之和为X,求X≤30的概率;
(2)设小明两次抽奖都选择方案甲或都选择方案乙,且都选择方案乙时,已算得,累计获得的购物代金券面额之和X1的数学期望E(X1)=24,问:小明选择这两种方案中的何种方案抽奖,累计获得的购物代金券面额之和的数学期望较大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在R上的函数满足:f(x)= ![]() ,且f(x+2)=f(x),g(x)=
,且f(x+2)=f(x),g(x)= ![]() ,则方程f(x)=g(x)在区间[﹣7,3]上的所有实数根之和为( )
,则方程f(x)=g(x)在区间[﹣7,3]上的所有实数根之和为( )
A.﹣9
B.﹣10
C.﹣11
D.﹣12
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com