解:(1)(lg50)
2+lg2×lg(50)
2+lg
22=lg
250+2lg2×lg50+lg
22
=(lg50+lg2)
2=(lg100)
2=2
2=4;
(2)因为
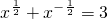
,所以
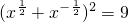
,即x+x
-1=7,
所以(x+x
-1)
2=49,则x
2+x
-2=47,所以

=9.
分析:(1)把中间项的真数的指数2拿到前面后构成完全平方式,进一步运用对数式的运算性质可求解;
(2)把已知条件两次平方后可求要求值的式子的分子和分母.
点评:本题考查了对数的运算性质,有理指数幂的化简与求值,解答(1)的关键是熟练运算性质,解答(2)的关键是想到把已知的等式两边平方,(1)是常规题型,(2)有一定技巧.

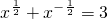 ,求
,求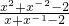 的值.
的值.