
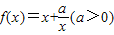 ,当x∈[1,3]时,f(x)的值域为A,且A⊆[n,m](n<m).
,当x∈[1,3]时,f(x)的值域为A,且A⊆[n,m](n<m).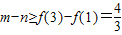 ,求得m-n的最小值.
,求得m-n的最小值.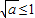 、
、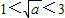 和
和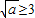 三种情况,分别求出a的取值范围,再取并集,即得所求.
三种情况,分别求出a的取值范围,再取并集,即得所求.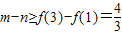 ,即m-n的最小值是
,即m-n的最小值是 .…(5分)
.…(5分)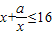 恒成立,即当x∈[1,3]时,a≤16x-x2恒成立,
恒成立,即当x∈[1,3]时,a≤16x-x2恒成立,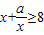 恒成立,即当x∈[1,3]时,a≥8x-x2恒成立,∴a≥(-x2+8x)max =15.…(9分)
恒成立,即当x∈[1,3]时,a≥8x-x2恒成立,∴a≥(-x2+8x)max =15.…(9分)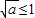 ,即0<a≤1时,
,即0<a≤1时,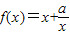 在[1,3]单调递增,
在[1,3]单调递增,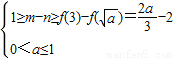 ,a无解.…(11分)
,a无解.…(11分)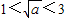 ,即1<a<9时,
,即1<a<9时,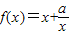 在
在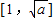 递减,在
递减,在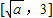 递增,
递增,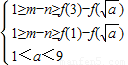 ,∴
,∴ ,
,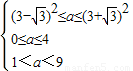 ,
,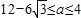 .…(13分)
.…(13分)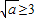 ,即a≥9时,函数f(x)在区间[1,3]上单调递减,
,即a≥9时,函数f(x)在区间[1,3]上单调递减,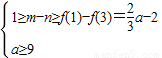 ,a无解;…(14分),
,a无解;…(14分),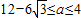 .…(16分)
.…(16分)

 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:高中数学 来源:2012-2013学年浙江省宁波市金兰合作组织高一(上)期中数学试卷(解析版) 题型:选择题
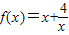 ,当x∈[1,3]时的值域为[n,m],则m-n的值是( )
,当x∈[1,3]时的值域为[n,m],则m-n的值是( )


查看答案和解析>>
科目:高中数学 来源:2012-2013学年浙江省宁波市金兰合作组织高一(上)期中数学试卷(解析版) 题型:选择题
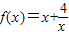 ,当x∈[1,3]时的值域为[n,m],则m-n的值是( )
,当x∈[1,3]时的值域为[n,m],则m-n的值是( )


查看答案和解析>>
科目:高中数学 来源:2009-2010学年湖北省孝感高中高三(上)7月综合测试数学试卷1(文科)(解析版) 题型:选择题
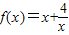 ,当x∈[1,3]时的值域为[n,m],则m-n的值是( )
,当x∈[1,3]时的值域为[n,m],则m-n的值是( )


查看答案和解析>>
科目:高中数学 来源:2012年黑龙江省哈尔滨九中高考数学三模试卷(文科)(解析版) 题型:选择题
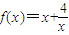 ,当x∈[1,3]时的值域为[n,m],则m-n的值是( )
,当x∈[1,3]时的值域为[n,m],则m-n的值是( )


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com