
【题目】在△ABC中,角A,B,C所对的边分别是a,b,c,且a=2,2cos2 ![]() +sinA=
+sinA= ![]() .
.
(1)若满足条件的△ABC有且只有一个,求b的取值范围;
(2)当△ABC的周长取最大值时,求b的值.
【答案】
(1)解:△ABC中,角A,B,C所对的边分别是a,b,c,且a=2,2cos2 ![]() +sinA=
+sinA= ![]() ,
,
∴2 ![]() +sinA=
+sinA= ![]() ,即 2
,即 2 ![]() +sinA=
+sinA= ![]() ,∴cosA﹣sinA=
,∴cosA﹣sinA= ![]() ,
,
平方可得sin2A= ![]() ,∴cosA+sinA=
,∴cosA+sinA= ![]() =
= ![]() ,
,
求得cosA= ![]() ,sinA=
,sinA= ![]() ∈(
∈( ![]() ,
, ![]() ),结合满足条件的△ABC有且只有一个,∴A∈(
),结合满足条件的△ABC有且只有一个,∴A∈( ![]() ,
, ![]() ).
).
∴由正弦定理可得 a=bsinA,即2= ![]() b,即 b=
b,即 b= ![]() ;或 a≥b,即0<b≤2,综上可得,b∈(0,2]∪{
;或 a≥b,即0<b≤2,综上可得,b∈(0,2]∪{ ![]() }.
}.
(2)解:由于△ABC的周长为a+b+c,
由余弦定理可得22=b2+c2﹣2bc ![]() =(b+c)2﹣
=(b+c)2﹣ ![]() bc≥(b+c)2﹣
bc≥(b+c)2﹣ ![]()
![]() =
= ![]() (b+c)2,
(b+c)2,
∴b+c≤ ![]() =2
=2 ![]() ,当且仅当b=c时,取等号,此时,三角形的周长为 2+b+c最大为2+2
,当且仅当b=c时,取等号,此时,三角形的周长为 2+b+c最大为2+2 ![]() ,
,
故此时b= ![]()
【解析】(1)由条件利用三角恒等变换求得cosA 和sinA 的值,结合满足条件的△ABC有且只有一个可得a=bsinA 或 a≥b,由此求得b的范围.(2)△ABC的周长为a+b+c,利用余弦定理、基本不等式求得周长2+b+c最大值为2+2 ![]() ,此时,b=
,此时,b= ![]() =c.
=c.
【考点精析】解答此题的关键在于理解正弦定理的定义的相关知识,掌握正弦定理:![]() ,以及对余弦定理的定义的理解,了解余弦定理:
,以及对余弦定理的定义的理解,了解余弦定理:![]() ;
;![]() ;
;![]() .
.


 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案科目:高中数学 来源: 题型:
【题目】某成衣批发店为了对一款成衣进行合理定价,将该款成衣按事先拟定的价格进行试销,得到了如下数据:
批发单价x(元) | 80 | 82 | 84 | 86 | 88 | 90 |
销售量y(件) | 90 | 84 | 83 | 80 | 75 | 68 |
(1)求回归直线方程 ![]() ,其中
,其中 ![]()
(2)预测批发单价定为85元时,销售量大概是多少件?
(3)假设在今后的销售中,销售量与批发单价仍然服从(1)中的关系,且该款成衣的成本价为40元/件,为使该成衣批发店在该款成衣上获得更大利润,该款成衣单价大约定为多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形ABCD与ABEF均为矩形,BC=BE=2AB,二面角E﹣AB﹣C的大小为 ![]() .现将△ACD绕着AC旋转一周,则在旋转过程中,( )
.现将△ACD绕着AC旋转一周,则在旋转过程中,( ) 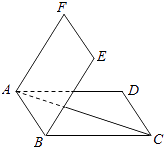
A.不存在某个位置,使得直线AD与BE所成的角为 ![]()
B.存在某个位置,使得直线AD与BE所成的角为 ![]()
C.不存在某个位置,使得直线AD与平面ABEF所成的角为 ![]()
D.存在某个位置,使得直线AD与平面ABEF所成的角为 ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin(2x+φ),其中φ为实数,若f(x)≤|f( ![]() )|对x∈R恒成立,且f(
)|对x∈R恒成立,且f( ![]() )>f(π),则f(x)的单调递增区间是( )
)>f(π),则f(x)的单调递增区间是( )
A.[kπ﹣ ![]() ,kπ+
,kπ+ ![]() ](k∈Z)
](k∈Z)
B.[kπ,kπ+ ![]() ](k∈Z)
](k∈Z)
C.[kπ+ ![]() ,kπ+
,kπ+ ![]() ](k∈Z)
](k∈Z)
D.[kπ﹣ ![]() ,kπ](k∈Z)
,kπ](k∈Z)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设{an}是等比数列,下列结论中正确的是( )
A.若a1+a2>0,则a2+a3>0
B.若a1+a3<0,则a1+a2<0
C.若0<a1<a2 , 则2a2<a1+a3
D.若a1<0,则(a2﹣a1)(a2﹣a3)>0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=﹣x2+2bx+c,设函数g(x)=|f(x)|在区间[﹣1,1]上的最大值为M.
(1)若b=2,试求出M;
(2)若M≥k对任意的b、c恒成立,试求k的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C所对应的边分别为a,b,c,且(2a﹣c)cosB=bcosC. (Ⅰ)求角B的大小;
(Ⅱ)若a=2,c=3,求sinC的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com