
【题目】已知抛物线 ![]() 和
和 ![]() 所围成的封闭曲线,给定点A(0,a),若在此封闭曲线上恰有三对不同的点,满足每一对点关于点A对称,则实数a的取值范围是 .
所围成的封闭曲线,给定点A(0,a),若在此封闭曲线上恰有三对不同的点,满足每一对点关于点A对称,则实数a的取值范围是 .
 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2+4x+a﹣5,g(x)=m4x﹣1﹣2m+7.
(1)若函数f(x)在区间[﹣1,1]上存在零点,求实数a的取值范围;
(2)当a=0时,若对任意的x1∈[1,2],总存在x2∈[1,2],使f(x1)=g(x2)成立,求实数m的取值范围;
(3)若y=f(x)(x∈[t,2])的置于为区间D,是否存在常数t,使区间D的长度为6﹣4t?若存在,求出t的值;若不存在,请说明理由. (注:区间[p,q]的长度q﹣p)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C的中心在原点,焦点在x轴上,离心率等于 ![]() ,它的一个短轴端点是(0,2
,它的一个短轴端点是(0,2 ![]() ).
). 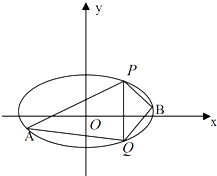
(1)求椭圆C的方程;
(2)P(2,3)、Q(2,﹣3)是椭圆上两点,A、B是椭圆位于直线PQ两侧的两动点,
①若直线AB的斜率为 ![]() ,求四边形APBQ面积的最大值;
,求四边形APBQ面积的最大值;
②当A、B运动时,满足∠APQ=∠BPQ,试问直线AB的斜率是否为定值,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆的中心在原点O,短轴长为 ![]() ,左焦点为F(﹣c,0)(c>0),直线
,左焦点为F(﹣c,0)(c>0),直线 ![]() 与x轴交于点A,且
与x轴交于点A,且 ![]() ,过点A的直线与椭圆相交于P,Q两点.
,过点A的直线与椭圆相交于P,Q两点. 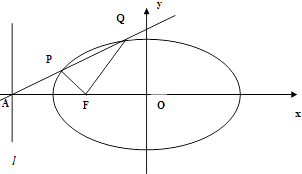
(1)求椭圆的方程.
(2)若 ![]() ,求直线PQ的方程.
,求直线PQ的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=Asin(ωx+)( ![]() )的部分图象如图所示.
)的部分图象如图所示. 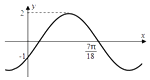
(1)求函数f(x)的解析式.
(2)函数y=f(x)的图象可以由y=sinx的图象变换后得到,请写出一种变换过程的步骤(注明每个步骤后得到新的函数解析式).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=2sin(2x+ ![]() ),g(x)=mcos(2x﹣
),g(x)=mcos(2x﹣ ![]() )﹣2m+3(m>0),若对任意x1∈[0,
)﹣2m+3(m>0),若对任意x1∈[0, ![]() ],存在x2∈[0,
],存在x2∈[0, ![]() ],使得g(x1)=f(x2)成立,则实数m的取值范围是( )
],使得g(x1)=f(x2)成立,则实数m的取值范围是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】据调查分析,若干年内某产品关税与市场供应量P的关系近似地满足:y=P(x)=2 ![]() ,(其中,t为关税的税率,且t∈[0,
,(其中,t为关税的税率,且t∈[0, ![]() ),x为市场价格,b,k为正常数),当t=
),x为市场价格,b,k为正常数),当t= ![]() 时的市场供应量曲线如图.
时的市场供应量曲线如图. 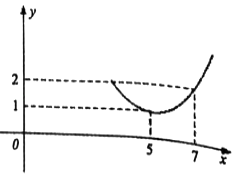
(Ⅰ)根据图象求b,k的值;
(Ⅱ)若市场需求量为Q(x)=2 ![]() ,当p=Q时的市场价格称为市场平衡价格,当市场平衡价格保持在10元时,求税率t的值.
,当p=Q时的市场价格称为市场平衡价格,当市场平衡价格保持在10元时,求税率t的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com