
【题目】“糖尿病”已经成为日渐多发的一种疾病,其具有危害性大且难以完全治愈的特征.为了更好的抑制“糖尿病”多发的势头,某社区卫生医疗机构针对所服务居民开展了免费测血糖活动,将随机抽取的10名居民均分为![]() ,
, ![]() 两组(
两组(![]() 组:4.3,5.1,4.6,4.1,4.9;
组:4.3,5.1,4.6,4.1,4.9; ![]() 组:5.1,4.9,4.0,4.0,4.5).
组:5.1,4.9,4.0,4.0,4.5).
(1)通过提供的数据请判断哪一组居民的血糖值更低;
(2)现从![]() 组的5名居民中随机选取2名,求这2名中至少有1名的血糖值低于4.5的概率.
组的5名居民中随机选取2名,求这2名中至少有1名的血糖值低于4.5的概率.
【答案】(1) ![]() 组居民的血糖值更低(2)
组居民的血糖值更低(2) ![]()
【解析】试题分析: (1)根据题中给出的数据分别计算A,B两组的平均数,比较可得结果;(2) 从![]() 组5名居民中随机选取2名,基本事件总数为10,这2名居民中至少有1名的血糖值低于4.5对立事件是这2名居民的视力都不低于4.5,列举出基本事件,根据古典概型求出概率,再求出事件的对立事件即可.
组5名居民中随机选取2名,基本事件总数为10,这2名居民中至少有1名的血糖值低于4.5对立事件是这2名居民的视力都不低于4.5,列举出基本事件,根据古典概型求出概率,再求出事件的对立事件即可.
试题解析:
(1)![]() 组5名居民血糖值的平均数
组5名居民血糖值的平均数![]() ,
,
![]() 组5名居民血糖值的平均数
组5名居民血糖值的平均数![]() ,
,
从计算结果看, ![]() 组居民的血糖值更低.
组居民的血糖值更低.
(2)从![]() 组5名居民中随机选取2名,基本事件总数为10,
组5名居民中随机选取2名,基本事件总数为10,
这2名居民中至少有1名的血糖值低于4.5对立事件是这2名居民的视力都不低于4.5,这2名居民的血糖值都不低于4.5,包含的基本事件有![]() ,
, ![]() ,
, ![]() ,
,
所以这2名居民的血糖值都不低于4.5的概率![]() .
.


科目:高中数学 来源: 题型:
【题目】已知向量 ![]() 与
与 ![]() .
.
(Ⅰ)若 ![]() 在
在 ![]() 方向上的投影为
方向上的投影为 ![]() ,求λ的值;
,求λ的值;
(Ⅱ)命题P:向量 ![]() 与
与 ![]() 的夹角为锐角;
的夹角为锐角;
命题q: ![]() ,其中向量
,其中向量 ![]() ,
, ![]() =(
=( ![]() )(λ,α∈R).若“p或q”为真命题,“p且q”为假命题,求λ的取值范围.
)(λ,α∈R).若“p或q”为真命题,“p且q”为假命题,求λ的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地最近十年对某商品的需求量逐年上升,下表是部分统计数据:
年份 | 2008 | 2010 | 2012 | 2014 | 2016 |
需要量(万件) | 236 | 246 | 257 | 276 | 286 |
(1)利用所给数据求年需求量y与年份x之间的回归直线方程 ![]() =
= ![]() x+
x+ ![]() ;
;
(2)预测该地2018年的商品需求量(结果保留整数).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】要测量底部不能到达的电视塔AB的高度,在C点测得塔顶A的仰角是45°,在D点测得塔顶A的仰角是30°,并测得水平面上的∠BCD=120°,CD=40m,则电视塔的高度为( ) 
A.40m
B.20m
C.305m
D.(20 ![]() ﹣40)m
﹣40)m
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】解答
(1)将一颗骰子(一种各个面上分别标有1,2,3,4,5,6个点的正方体玩具)先后抛掷2次,以分别得到的点数(m,n)作为点P的坐标(m,n),求:点P落在区域 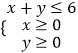 内的概率;
内的概率;
(2)在区间[1,6]上任取两个实数(m,n),求:使方程x2+mx+n2=0有实数根的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,设命题p:椭圆C: ![]() +
+ ![]() =1的焦点在x轴上;命题q:直线l:x﹣y+m=0与圆O:x2+y2=9有公共点. 若命题p、命题q中有且只有一个为真命题,求实数m的取值范围.
=1的焦点在x轴上;命题q:直线l:x﹣y+m=0与圆O:x2+y2=9有公共点. 若命题p、命题q中有且只有一个为真命题,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
以直角坐标系的原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴建立坐标系,已知点
轴的正半轴为极轴建立坐标系,已知点![]() 的直角坐标为
的直角坐标为![]() ,若直线
,若直线![]() 的极坐标方程为
的极坐标方程为![]() .曲线
.曲线![]() 的参数方程是
的参数方程是![]() (
(![]() 为参数).
为参数).
(1)求直线![]() 和曲线
和曲线![]() 的普通方程;
的普通方程;
(2)设直线![]() 和曲线
和曲线![]() 交于
交于![]() 两点,求
两点,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin(ωx+φ)(ω>0,|φ|< ![]() )的部分图象如图所示.
)的部分图象如图所示.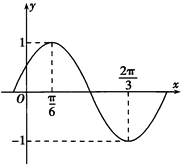
(1)求函数f(x)的解析式,并写出f(x)的单调减区间;
(2)已知△ABC的内角分别是A,B,C,A为锐角,且f ![]() ,求cosA的值.
,求cosA的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com