
【题目】已知Sn是正项数列{an}的前n项和,且满足a1=4,6Sn=an2+3an+λ(n∈N*,λ∈R),设bn=(n﹣μ)an,若b2是数列{bn}中唯一的最小项,则实数μ的取值范围是_____.
【答案】(![]() ,
,![]() )
)
【解析】
先根据数列满足![]() ,
,![]() ,求出其通项公式,进而求出
,求出其通项公式,进而求出![]() 的通项公式,再结合
的通项公式,再结合![]() 是数列
是数列![]() 中唯一的最小项,即可求出实数
中唯一的最小项,即可求出实数![]() 的取值范围.
的取值范围.
∵Sn是正项数列{an}的前n项和,且满足a1=4,6Sn=an2+3an+λ(n∈N*,λ∈R),
∴6×4=42+3×4+λλ=﹣4,
∴6Sn=an2+3an﹣4,①
6Sn﹣1=an﹣12+3an﹣1﹣4,②
①﹣②6an=an2+3an﹣4﹣(an﹣12+3an﹣1﹣4)(an+an﹣1)(an﹣an﹣1﹣3)=0,
∵an>0an﹣an﹣1﹣3=0数列{an}是首项为4,公差为3的等差数列,
∴an=4+3(n﹣1)=3n+1,
∴bn=(n﹣μ)an=(n﹣μ)(3n+1)=3n2+(1﹣3μ)n﹣μ;
∵b2是数列{bn}中唯一的最小项,
∴其对称轴![]() ∈(
∈(![]() ,
,![]() )
)![]() .
.
故答案为:(![]() ,
,![]() ).
).


 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点为
的焦点为![]() ,过点
,过点![]() 作斜率为
作斜率为![]() 的直线交抛物线于
的直线交抛物线于![]() 两点.
两点.
(1)若![]() ,求
,求![]() 的面积;
的面积;
(2)过点![]() 分别作抛物线
分别作抛物线![]() 的两条切线
的两条切线![]() ,且直线
,且直线![]() 与直线
与直线![]() 相交于点
相交于点![]() ,问:点
,问:点![]() 是否在某条定直线
是否在某条定直线![]() 上?若在,求该定直线
上?若在,求该定直线![]() 的方程;若不在,请说明理由.
的方程;若不在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 离心率为
离心率为![]() ,四个顶点构成的四边形的面积是4.
,四个顶点构成的四边形的面积是4.
(1)求椭圆C的标准方程;
(2)若直线![]() 与椭圆C交于P,Q均在第一象限,直线OP,OQ的斜率分别为
与椭圆C交于P,Q均在第一象限,直线OP,OQ的斜率分别为![]() ,
,![]() ,且
,且![]() (其中O为坐标原点).证明:直线l的斜率k为定值.
(其中O为坐标原点).证明:直线l的斜率k为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABCA1B1C1中,AB=AC,A1C⊥BC1,AB1⊥BC1,D,E分别是AB1和BC的中点.
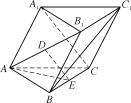
求证:(1)DE∥平面ACC1A1;
(2)AE⊥平面BCC1B1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数g(x)=﹣4sin2(![]() )+2图象上点的横坐标缩短到原来的
)+2图象上点的横坐标缩短到原来的![]() 倍(纵坐标不变),再向右平移
倍(纵坐标不变),再向右平移![]() 个单位长度,得到函数f(x)的图象,则下列说法正确的是( )
个单位长度,得到函数f(x)的图象,则下列说法正确的是( )
A.函数f(x)在区间[![]() ,
,![]() ]上单调递减
]上单调递减
B.函数f(x)的最小正周期为2π
C.函数f(x)在区间[![]() ,
,![]() ]的最小值为
]的最小值为![]()
D.x![]() 是函数f(x)的一条对称轴
是函数f(x)的一条对称轴
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).M是曲线
为参数).M是曲线![]() 上的动点,将线段OM绕O点顺时针旋转
上的动点,将线段OM绕O点顺时针旋转![]() 得到线段ON,设点N的轨迹为曲线
得到线段ON,设点N的轨迹为曲线![]() .以坐标原点O为极点,
.以坐标原点O为极点,![]() 轴正半轴为极轴建立极坐标系.
轴正半轴为极轴建立极坐标系.
(1)求曲线![]() 的极坐标方程;
的极坐标方程;
(2)在(1)的条件下,若射线![]() 与曲线
与曲线![]() 分别交于A, B两点(除极点外),且有定点
分别交于A, B两点(除极点外),且有定点![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,已知椭圆
,已知椭圆![]() 上存在点
上存在点![]() ,使
,使![]() ,且这样的点
,且这样的点![]() 有且只有两个.
有且只有两个.
(1)求椭圆![]() 的离心率;
的离心率;
(2)过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点,且
两点,且![]() ,
,![]() 是坐标原点,求
是坐标原点,求![]() 的面积取得最大值时的椭圆方程.
的面积取得最大值时的椭圆方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点F是抛物线C:y2=2px(p>0)的焦点,若点P(x0,4)在抛物线C上,且![]() .
.
(1)求抛物线C的方程;
(2)动直线l:x=my+1(m![]() R)与抛物线C相交于A,B两点,问:在x轴上是否存在定点D(t,0)(其中t≠0),使得kAD+kBD=0,(kAD,kBD分别为直线AD,BD的斜率)若存在,求出点D的坐标;若不存在,请说明理由.
R)与抛物线C相交于A,B两点,问:在x轴上是否存在定点D(t,0)(其中t≠0),使得kAD+kBD=0,(kAD,kBD分别为直线AD,BD的斜率)若存在,求出点D的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),直线
为参数),直线![]() 的参数方程为
的参数方程为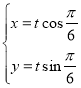 (
(![]() 为参数).以坐标原点为极点,
为参数).以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系.
轴正半轴为极轴建立极坐标系.
(1)分别写出曲线![]() 和曲线
和曲线![]() 的极坐标方程;
的极坐标方程;
(2)P为曲线![]() 上的任意一点,过P向曲线
上的任意一点,过P向曲线![]() 引两条切线PA、PB,当
引两条切线PA、PB,当![]() 最大时,求P点的极坐标.
最大时,求P点的极坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com