
从某节能灯生产在线随机抽取100件产品进行寿命试验,按连续使用时间(单位:天)共分5组,得到频率分布直方图如图.
(I)以分组的中点资料作为平均数据,用样本估计该生产线所生产的节能灯的预期连续使用寿命;
(II)为了分析使用寿命差异较大的产品,从使用寿命低于200天和高于350天的产品中用分层抽样的方法共抽取6件,求样品A被抽到的概率。
(I)280天(II)
解析试题分析:(Ⅰ)样本数据的平均数为:
175×0.05+225×0.15+275×0.55+325×0.15+375×0.1=280.
因此,该生产线所生产的节能灯的预期连续使用寿命为280天. …5分
(Ⅱ)使用寿命低于200天的一组中应抽取 . …7分
. …7分
记使用寿命低于200天的5件产品A,B,C,D,E.
从中选出2件的不同情形为:
AB,AC,AD,AE,
BC,BD,BE,
CD,CE,
DE,
共10种可能.
其中某产品A被抽到的概率为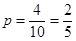 .
.
考点:频率分布直方图及分层抽样古典概率
点评:频率分布直方图中每一个小矩形的面积等于该组的频率,古典概型概率的求解需找到所有基本事件总数及满足题意要求的基本事件种数,然后求其比值


科目:高中数学 来源: 题型:解答题
袋中装有大小相同的2个白球和3个黑球.
(1)采取放回抽样方式,从中依次摸出两个球,求两球颜色不同的概率;
(2)采取不放回抽样方式,从中依次摸出两个球,记 为摸出两球中白球的个数,
为摸出两球中白球的个数,
求 的期望.
的期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
“H7N9禽流感”问题越来越引起社会关注,我校对高一600名学生进行了一次“H7N9禽流感”知识测试,并从中抽取了部分学生的成绩(满分100分)作为样本,绘制了下面尚未完成的频率分布表和频率分布直方图.
(1)填写答题卡频率分布表中的空格,补全频率分布直方图,并标出每个小矩形对应的纵轴数据;
(2)试估计该年段成绩在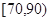 段的有多少人;
段的有多少人;
(3)请你估算该年级的平均分.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
由于某高中建设了新校区,为了交通方便要用三辆通勤车从老校区把教师接到新校区.已知从新校区到老校区有两条公路,汽车走一号公路堵车的概率为 ,不堵车的概率为
,不堵车的概率为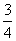 ;汽车走二号公路堵车的概率为p,不堵车的概率为1-p,若甲、乙两辆汽车走一号公路,丙汽车由于其他原因走二号公路,且三辆车是否堵车相互之间没有影响.
;汽车走二号公路堵车的概率为p,不堵车的概率为1-p,若甲、乙两辆汽车走一号公路,丙汽车由于其他原因走二号公路,且三辆车是否堵车相互之间没有影响.
(Ⅰ)若三辆汽车中恰有一辆汽车被堵的概率为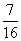 ,求走二号公路堵车的概率;
,求走二号公路堵车的概率;
(Ⅱ)在(Ⅰ)的条件下,求三辆汽车中被堵车辆的个数ξ的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在某校组织的一次篮球定点投篮测试中,规定每人最多投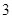 次,每次投篮的结果相互独立.在
次,每次投篮的结果相互独立.在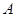 处每投进一球得
处每投进一球得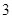 分,在
分,在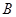 处每投进一球得
处每投进一球得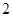 分,否则得
分,否则得 分. 将学生得分逐次累加并用
分. 将学生得分逐次累加并用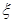 表示,如果
表示,如果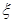 的值不低于
的值不低于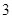 分就认为通过测试,立即停止投篮,否则继续投篮,直到投完三次为止.投篮的方案有以下两种:方案1:先在
分就认为通过测试,立即停止投篮,否则继续投篮,直到投完三次为止.投篮的方案有以下两种:方案1:先在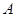 处投一球,以后都在
处投一球,以后都在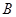 处投;方案2:都在
处投;方案2:都在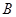 处投篮.甲同学在
处投篮.甲同学在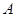 处投篮的命中率为
处投篮的命中率为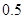 ,在
,在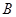 处投篮的命中率为
处投篮的命中率为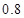 .
.
(Ⅰ)甲同学选择方案1.
求甲同学测试结束后所得总分等于4的概率;
求甲同学测试结束后所得总分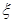 的分布列和数学期望
的分布列和数学期望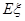 ;
;
(Ⅱ)你认为甲同学选择哪种方案通过测试的可能性更大?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
一个袋中装有大小相同的球10个,其中红球8个,黑球2个,现从袋中有放回地取球,每次随机取1个. 求:
(1)连续取两次都是红球的概率;
(2)如果取出黑球,则取球终止,否则继续取球,直到取出黑球,但取球次数最多不超过4次,求取到黑球的概率。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某广场上有4盏装饰灯,晚上每盏灯都随机地闪烁红灯或绿灯,每盏灯出现红灯的概率都是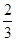 ,出现绿灯的概率都是
,出现绿灯的概率都是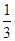 .记这4盏灯中出现红灯的数量为
.记这4盏灯中出现红灯的数量为 ,当这排装饰灯闪烁一次时:
,当这排装饰灯闪烁一次时:
(1)求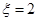 时的概率;(2)求
时的概率;(2)求 的数学期望.
的数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com