
【题目】如图:在四棱锥![]() 中,底面
中,底面![]() 是菱形,
是菱形, ![]() ,
, ![]() 平面
平面![]() ,点
,点![]() 为
为![]() 的中点,且
的中点,且![]() .
.
(1)证明: ![]() 面
面![]() ;
;
(2)求三棱锥![]() 的体积;
的体积;
(3)在线段![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() 平面
平面![]() ;若存在,求出
;若存在,求出![]() 的长;若不存在,说明理由.
的长;若不存在,说明理由.
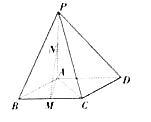
【答案】证明:(I)因为ABCD为菱形,所以AB=BC
又∠ABC=60°,所以AB=BC=AC, ………………1分
又M为BC中点,所以BC⊥AM ………………2分
而PA⊥平面ABCD,BC![]() 平面ABCD,所以PA⊥BC ………………4分
平面ABCD,所以PA⊥BC ………………4分
又PA∩AM=A,所以BC⊥平面AMN ………………5分
(II)因为![]() ………………6分
………………6分
又PA⊥底面ABCD,PA=2,所以AN=1
所以,三棱锥N—AMC的体积![]() ………………8分
………………8分
![]() ………………9分
………………9分
(III)存在 ………………10分
取PD中点E,连结NE,EC,AE,
因为N,E分别为PA,PD中点,所以![]() ………………11分
………………11分
又在菱形ABCD中, ![]()
所以NE ![]() ,即MCEN是平行四边形 ………………12分
,即MCEN是平行四边形 ………………12分
所以,NM//EC,
又EC![]() 平面ACE,NM
平面ACE,NM![]() 平面ACE
平面ACE
所以MN//平面ACE, ………………13分
即在PD上存在一点E,使得NM//平面ACE,
此时![]()
【解析】略


科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,二次函数
中,二次函数![]() 的图象与
的图象与![]() 轴交于
轴交于![]() ,
, ![]() 两点,点
两点,点![]() 的坐标为
的坐标为![]() .当
.当![]() 变化时,解答下列问题:
变化时,解答下列问题:
(1)以![]() 为直径的圆能否经过点
为直径的圆能否经过点![]() ?说明理由;
?说明理由;
(2)过![]() ,
, ![]() ,
, ![]() 三点的圆在
三点的圆在![]() 轴上截得的弦长是否为定值?若是,则求出该定值;若不是,请说明理由.
轴上截得的弦长是否为定值?若是,则求出该定值;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 与抛物线
与抛物线![]() 共焦点
共焦点![]() ,抛物线上的点M到y轴的距离等于
,抛物线上的点M到y轴的距离等于![]() ,且椭圆与抛物线的交点Q满足
,且椭圆与抛物线的交点Q满足![]() .
.
(I)求抛物线的方程和椭圆的方程;
(II)过抛物线上的点![]() 作抛物线的切线
作抛物线的切线![]() 交椭圆于
交椭圆于![]() 、
、![]() 两点,求此切线在x轴上的截距的取值范围.
两点,求此切线在x轴上的截距的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市100户居民的月平均用电量(单位:度),以![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 分组的频率分布直方图如图所示.
分组的频率分布直方图如图所示.
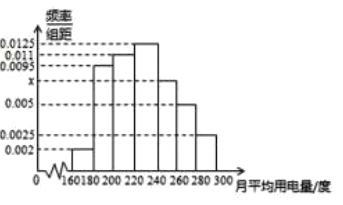
(1)求直方图中![]() 的值;
的值;
(2)求月平均用电量的众数和中位数;
(3)在月平均用电量在![]() ,
, ![]() ,
, ![]() 的三组用户中,用分层抽样的方法抽取10户居民,则月平均用电量在
的三组用户中,用分层抽样的方法抽取10户居民,则月平均用电量在![]() 的用户中应抽取多少户?
的用户中应抽取多少户?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,已知曲线
中,已知曲线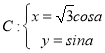 (
(![]() 为参数),在以原点
为参数),在以原点![]() 为极点,
为极点, ![]() 轴的非负半轴为极轴建立的极坐标系中,直线的极坐标方程为:
轴的非负半轴为极轴建立的极坐标系中,直线的极坐标方程为: ![]() .
.
(Ⅰ)求曲线![]() 的普通方程和直线的直角坐标方程;
的普通方程和直线的直角坐标方程;
(Ⅱ)过点![]() 且与直线平行的直线
且与直线平行的直线![]() 交
交![]() 于
于![]() ,
, ![]() 两点,求点
两点,求点![]() 到
到![]() ,
, ![]() 两点的距离之积.
两点的距离之积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市积极倡导学生参与绿色环保活动,其中代号为“环保卫士—12369”的绿色环保活动小组对2014年1月—2014年12月(一年)内空气质量指数![]() 进行监测,下表是在这一年随机抽取的100天的统计结果:
进行监测,下表是在这一年随机抽取的100天的统计结果:
指数API | [0,50] | (50,100] | (100,150] | (150,200] | (200,250] | (250,300] | >300 |
空气质量 | 优 | 良 | 轻微污染 | 轻度污染 | 中度污染 | 中重度污染 | 重度污染 |
天数 | 4 | 13 | 18 | 30 | 9 | 11 | 15 |
(1)若某市某企业每天由空气污染造成的经济损失![]() (单位:元)与空气质量指数
(单位:元)与空气质量指数![]() (记为
(记为![]() )的关系为:
)的关系为: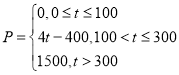 ,在这一年内随机抽取一天,估计该天经济损失
,在这一年内随机抽取一天,估计该天经济损失![]() 元的概率;
元的概率;
(2)若本次抽取的样本数据有30天是在供暖季节,其中有8天为重度污染,![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为某市本年度空气重度污染与供暖有关?
的把握认为某市本年度空气重度污染与供暖有关?
非重度污染 | 重度污染 | 合计 | |
供暖季 | |||
非供暖季节 | |||
合计 | 100 |
下面临界值表供参考.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
参考公式:![]() ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的离心率为
的离心率为![]() ,顺次连接椭圆
,顺次连接椭圆![]() 的四个顶点得到的四边形的面积为16.
的四个顶点得到的四边形的面积为16.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)过椭圆![]() 的顶点
的顶点![]() 的直线
的直线![]() 交椭圆于另一点
交椭圆于另一点![]() ,交
,交![]() 轴于点
轴于点![]() ,若
,若![]() 、
、![]() 、
、![]() 成等比数列,求直线
成等比数列,求直线![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,点
,点![]() 在函数
在函数![]() 图像上;
图像上;
(1)证明![]() 是等差数列;
是等差数列;
(2)若函数![]() ,数列
,数列![]() 满足
满足![]() ,记
,记![]() ,求数列
,求数列![]() 前
前![]() 项和
项和![]() ;
;
(3)是否存在实数![]() ,使得当
,使得当![]() 时,
时, ![]() 对任意
对任意![]() 恒成立?若存在,求出最大的实数
恒成立?若存在,求出最大的实数![]() ,若不存在,说明理由.
,若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com