
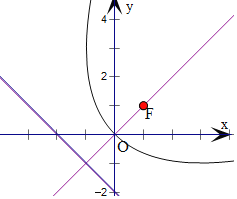
【题目】已知抛物线Γ的准线方程为![]() .焦点为
.焦点为![]() .
.
(1)求证:抛物线Γ上任意一点![]() 的坐标
的坐标![]() 都满足方程:
都满足方程:![]()
(2)请求出抛物线Γ的对称性和范围,并运用以上方程证明你的结论;
(3)设垂直于![]() 轴的直线与抛物线交于
轴的直线与抛物线交于![]() 两点,求线段
两点,求线段![]() 的中点
的中点![]() 的轨迹方程.
的轨迹方程.
【答案】(1)证明见解析(2)关于![]() 对称
对称![]() .证明见解析(3)
.证明见解析(3)![]() (在抛物线内)
(在抛物线内)
【解析】
(1)由抛物线的定义可得|PF|=d(d为P到准线的距离),运用两点的距离公式和点到直线的距离公式,化简可得所求轨迹方程;
(2)由抛物线的方程的特点,考虑点关于直线y=x的对称点的特征和对称轴与准线和抛物线的交点的关系,以及直线和抛物线相切的特点,可得所求范围;
(3)设垂直于x轴的直线为x=t,代入抛物线的方程x2﹣2xy+y2﹣8x﹣8y=0,运用韦达定理和中点坐标公式,以及参数方程化为普通方程可得所求轨迹方程.
(1)抛物线Γ的准线方程为x+y+2=0,焦点为F(1,1),
抛物线Γ上任意一点P的坐标(x,y),由抛物线的定义可得|PF|=d(d为P到准线的距离),即为![]() ,两边平方化简可得x2﹣2xy+y2﹣8x﹣8y=0;
,两边平方化简可得x2﹣2xy+y2﹣8x﹣8y=0;
(2)抛物线关于y=x对称,顶点为(0,0),范围为x≥﹣1,y≥﹣1,
由方程x2﹣2xy+y2﹣8x﹣8y=0,
设抛物线上任一点(x,y)关于直线y=x对称的点为(y,x),满足原方程,
则抛物线关于直线y=x对称;
由直线y﹣1=x﹣1即y=x,联立x+y+2=0,解得x=y=﹣1,
可得抛物线的顶点为(0,0);
由x=﹣1和x2﹣2xy+y2﹣8x﹣8y=0联立可得切点为(﹣1,3),
同样由y=﹣1和x2﹣2xy+y2﹣8x﹣8y=0联立可得切点为(3,﹣1),
可得抛物线的范围为x≥﹣1,y≥﹣1;
(3)设垂直于x轴的直线为x=t,代入抛物线的方程x2﹣2xy+y2﹣8x﹣8y=0,
可得t2﹣(2t+8)y+ t2﹣8t=0,
设A(t,y1),B(t,y2),可得y1+y2=2t+8,
则AB的中点为(t,t+4),
则AB的中点的轨迹方程为直线y=x+4(在抛物线内).


科目:高中数学 来源: 题型:
【题目】2018年8月8日是我国第十个全民健身日,其主题是:新时代全民健身动起来。某市为了解全民健身情况,随机从某小区居民中抽取了40人,将他们的年龄分成7段:[10,20),[20,30),[30,40),[40,50),[50,60),[60,70),[70,80]后得到如图所示的频率分布直方图。

(1)试求这40人年龄的平均数、中位数的估计值;
(2)(i)若从样本中年龄在[50,70)的居民中任取2人赠送健身卡,求这2人中至少有1人年龄不低于60岁的概率;
(ⅱ)已知该小区年龄在[10,80]内的总人数为2000,若18岁以上(含18岁)为成年人,试估计该小区年龄不超过80岁的成年人人数。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在正方形![]() 中,
中,![]() 是
是![]() 的中点,点
的中点,点![]() 在线段
在线段![]() 上,且
上,且![]() .若将
.若将![]() 分别沿
分别沿![]() 折起,使
折起,使![]() 两点重合于点
两点重合于点![]() ,如图2.
,如图2.
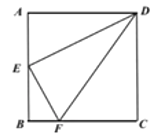
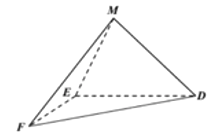
图1 图2
(1)求证:![]() 平面
平面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为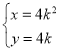 (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 和曲线
和曲线![]() 的普通方程;
的普通方程;
(2)已知点![]() ,且直线
,且直线![]() 和曲线
和曲线![]() 交于
交于![]() 两点,求
两点,求![]() 的值
的值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 各项均为正数,
各项均为正数,![]() 为其前
为其前![]() 项的和,且
项的和,且![]() 成等差数列.
成等差数列.
(1)写出![]() 、
、![]() 、
、![]() 的值,并猜想数列
的值,并猜想数列![]() 的通项公式
的通项公式![]() ;
;
(2)证明(1)中的猜想;
(3)设![]() ,
,![]() 为数列
为数列![]() 的前
的前![]() 项和.若对于任意
项和.若对于任意![]() ,都有
,都有![]() ,求实数
,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,曲线![]() (α为参数)经过伸缩变换
(α为参数)经过伸缩变换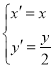 得到曲线C2.以坐标原点为极点,x轴正半轴为极轴建立极坐标系.
得到曲线C2.以坐标原点为极点,x轴正半轴为极轴建立极坐标系.
(1)求C2的普通方程;
(2)设曲线C3的极坐标方程为![]() ,且曲线C3与曲线C2相交于M,N两点,点P(1,0),求
,且曲线C3与曲线C2相交于M,N两点,点P(1,0),求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设有二元关系![]() ,已知曲线
,已知曲线![]() .
.
(1)若![]() 时,正方形
时,正方形![]() 的四个顶点均在曲线
的四个顶点均在曲线![]() 上,求正方形
上,求正方形![]() 的面积;
的面积;
(2)设曲线![]() 与
与![]() 轴的交点是
轴的交点是![]() ,抛物线
,抛物线![]() 与
与![]() 轴的交点是
轴的交点是![]() ,直线
,直线![]() 与曲线
与曲线![]() 交于
交于![]() ,直线
,直线![]() 与曲线
与曲线![]() 交于
交于![]() ,求证直线
,求证直线![]() 过定点,并求该定点的坐标;
过定点,并求该定点的坐标;
(3)设曲线![]() 与
与![]() 轴的交点是
轴的交点是![]() ,
,![]() ,可知动点
,可知动点![]() 在某确定的曲线
在某确定的曲线![]() 上运动,曲线
上运动,曲线![]() 上与上述曲线
上与上述曲线![]() 在
在![]() 时共有4个交点,其坐标分别是
时共有4个交点,其坐标分别是![]() 、
、![]() 、
、![]() 、
、![]() ,集合
,集合![]() 的所有非空子集设为
的所有非空子集设为![]() ,将
,将![]() 中的所有元素相加(若
中的所有元素相加(若![]() 只有一个元素,则和是其自身)得到255个数
只有一个元素,则和是其自身)得到255个数![]() ,求所有正整数
,求所有正整数![]() 的值,使得
的值,使得![]() 是一个与变数
是一个与变数![]() 及变数
及变数![]() 均无关的常数.
均无关的常数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学生对函数![]() 的性质进行研究,得出如下的结论:
的性质进行研究,得出如下的结论:
![]() 函数在
函数在![]() 上单调递减,在
上单调递减,在![]() 上单调递增;
上单调递增;
![]() 点
点![]() 是函数图象的一个对称中心;
是函数图象的一个对称中心;
![]() 函数图象关于直线
函数图象关于直线![]() 对称;
对称;
![]() 存在常数
存在常数![]() ,使
,使![]() 对一切实数x均成立,
对一切实数x均成立,
其中正确命题的个数是( )
A.1B.2C.3D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com