
(05年广东卷)(14分)
在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 上异于坐标原点
上异于坐标原点![]() 的两不同动点A、B满足
的两不同动点A、B满足![]() (如图4所示)
(如图4所示)
(Ⅰ)求![]() 得重心
得重心![]() (即三角形三条中线的交点)
(即三角形三条中线的交点)
的轨迹方程;
(Ⅱ)![]() 的面积是否存在最小值?若存在,请求出
的面积是否存在最小值?若存在,请求出
最小值;若不存在,请说明理由.

解析: 解法一:
(Ⅰ)∵直线![]() 的斜率显然存在,∴设直线
的斜率显然存在,∴设直线![]() 的方程为
的方程为![]() ,
,
![]() ,依题意得
,依题意得
![]() ,①
,①
∴![]() ,②
,② ![]() ③
③
∵![]() ,∴
,∴![]() ,即
,即 ![]() ,④
,④
由③④得,![]() ,∴
,∴![]()
∴设直线![]() 的方程为
的方程为![]()
∴①可化为 ![]() ,∴
,∴![]() ⑤,
⑤,
设![]() 的重心G为
的重心G为![]() ,则
,则
![]() ⑥ ,
⑥ , ![]() ⑦,
⑦,
由⑥⑦得 ![]() ,即
,即![]() ,这就是
,这就是![]() 得重心
得重心![]() 的轨迹方程.
的轨迹方程.
(Ⅱ)由弦长公式得![]()
把②⑤代入上式,得 ![]() ,
,
设点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,则
,则![]() ,
,
∴ ![]() ,
,
∴ 当![]() ,
,![]() 有最小值,
有最小值,
∴![]() 的面积存在最小值,最小值是
的面积存在最小值,最小值是![]() .
.
解法二:
(Ⅰ)∵ AO⊥BO, 直线![]() ,
,![]() 的斜率显然存在,
的斜率显然存在,
∴设AO、BO的直线方程分别为![]() ,
,![]() ,
,
设![]() ,
,![]() ,依题意可得
,依题意可得
由![]() 得
得 ![]() ,由
,由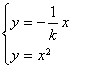 得
得 ![]() ,
,
设![]() 的重心G为
的重心G为![]() ,则
,则
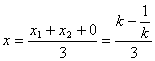 ① ,
① , 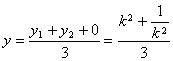 ②,
②,
由①②可得,![]() ,即为所求的轨迹方程.
,即为所求的轨迹方程.
(Ⅱ)由(Ⅰ)得,![]() ,
,![]() ,
,
∴![]()
![]()
![]() ,
,
当且仅当![]() ,即
,即![]() 时,
时,![]() 有最小值,
有最小值,
∴![]() 的面积存在最小值,最小值是
的面积存在最小值,最小值是![]() .
.
解法三:(I)设△AOB的重心为G(x , y) ,A(x1, y1),B(x2 , y2 ),则
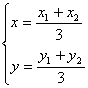 …(1)
…(1)
不过∵OA⊥OB ,
∴![]() ,即
,即![]() , …(2)
, …(2)
又点A,B在抛物线上,有![]() ,
,
代入(2)化简得![]() ,
,
∴![]() ,
,
∴所以重心为G的轨迹方程为![]() ,
,
(II)![]() ,
,
由(I)得![]() ,
,
当且仅当![]() 即
即![]() 时,等号成立,
时,等号成立,
所以△AOB的面积存在最小值,存在时求最小值1 .


 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案科目:高中数学 来源: 题型:
(09年江苏百校样本分析)(10分)挑选空军飞行学员可以说是“万里挑一”,要想通过需过“五关”――目测、初检、复检、文考、政审等. 某校甲、乙、丙三个同学都顺利通过了前两关,有望成为光荣的空军飞行学员. 根据分析,甲、乙、丙三个同学能通过复检关的概率分别是0.5,0.6,0.75,能通过文考关的概率分别是0.6,0.5,0.4,通过政审关的概率均为1.后三关相互独立.
(1)求甲、乙、丙三个同学中恰有一人通过复检的概率;
(2)设通过最后三关后,能被录取的人数为![]() ,求随机变量
,求随机变量![]() 的期望
的期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
(08年莆田四中一模理) (14分)
由函数![]() 确定数列
确定数列![]() ,
,![]() ,若函数
,若函数![]() 的反函数
的反函数![]() 能确定数列
能确定数列![]() ,
,![]() ,则称数列
,则称数列![]() 是数列
是数列![]() 的“反数列”。
的“反数列”。
(1)若函数![]() 确定数列
确定数列![]() 的反数列为
的反数列为![]() ,求
,求![]() 的通项公式;
的通项公式;
(2)对(1)中![]() ,不等式
,不等式![]() 对任意的正整数
对任意的正整数![]() 恒成立,求实数
恒成立,求实数![]() 的范围;
的范围;
(3)设![]() ,若数列
,若数列![]() 的反数列为
的反数列为![]() ,
,![]() 与
与![]() 的公共项组成的数列为
的公共项组成的数列为![]() ;求数列
;求数列![]() 前
前![]() 项和
项和![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com