
【题目】已知函数![]() .
.
(1)求函数![]() 的单调区间;
的单调区间;
(2)若关于![]() 的不等式
的不等式![]() 恒成立,求整数
恒成立,求整数![]() 的最小值.
的最小值.
【答案】(1) 当![]() 时,
时,![]() 的单调递增区间为
的单调递增区间为![]() ,无减区间,
,无减区间,
当![]() 时,
时,![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() ;(2)2.
;(2)2.
【解析】试题分析:
(1)首先对函数求导,然后对参数分类讨论可得当![]() 时,
时,![]() 的单调递增区间为
的单调递增区间为![]() ,无减区间,
,无减区间,
当![]() 时,
时,![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() ;
;
(2)将原问题转化为![]() 在
在![]() 上恒成立,考查函数
上恒成立,考查函数![]() 的性质可得整数
的性质可得整数![]() 的最小值是2.
的最小值是2.
试题解析:
(1)![]() ,函数
,函数![]() 的定义域为
的定义域为![]() .
.
当![]() 时,
时,![]() ,则
,则![]() 在
在![]() 上单调递增,
上单调递增,
当![]() 时,令
时,令![]() ,则
,则![]() 或
或![]() (舍负),
(舍负),
当![]() 时,
时,![]() ,
,![]() 为增函数,
为增函数,
当![]() 时,
时,![]() ,
,![]() 为减函数,
为减函数,
∴当![]() 时,
时,![]() 的单调递增区间为
的单调递增区间为![]() ,无减区间,
,无减区间,
当![]() 时,
时,![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() .
.
(2)解法一:由![]() 得
得![]() ,
,
∵![]() ,
,
∴原命题等价于![]() 在
在![]() 上恒成立,
上恒成立,
令![]() ,
,
则![]() ,
,
令![]() ,则
,则![]() 在
在![]() 上单调递增,
上单调递增,
由![]() ,
,![]() ,
,
∴存在唯一![]() ,使
,使![]() ,
,![]() .
.
∴当![]() 时,
时,![]() ,
,![]() 为增函数,
为增函数,
当![]() 时,
时,![]() ,
,![]() 为减函数,
为减函数,
∴![]() 时,
时,![]() ,
,
∴![]() ,
,
又![]() ,则
,则![]() ,
,
由![]() ,所以
,所以![]() .
.
故整数![]() 的最小值为2.
的最小值为2.
解法二:![]() 得,
得,
![]() ,
,
令![]() ,
,
![]() ,
,
①![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递减,
上单调递减,
∵![]() ,∴该情况不成立.
,∴该情况不成立.
②![]() 时,
时,![]()
当![]() 时,
时,![]() ,
,![]() 单调递减;
单调递减;
当![]() 时,
时,![]() ,
,![]() 单调递增,
单调递增,
∴![]() ,
,
![]() 恒成立
恒成立![]() ,
,
即![]() .
.
令![]() ,显然
,显然![]() 为单调递减函数.
为单调递减函数.
由![]() ,且
,且![]() ,
,![]() ,
,
∴当![]() 时,恒有
时,恒有![]() 成立,
成立,
故整数![]() 的最小值为2.
的最小值为2.
综合①②可得,整数![]() 的最小值为2.
的最小值为2.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】函数f(x)=sin(ωx+ ![]() )(ω>0)的图象的相邻两条对称轴间的距离是
)(ω>0)的图象的相邻两条对称轴间的距离是 ![]() .若将函数f(x)的图象向右平移
.若将函数f(x)的图象向右平移 ![]() 个单位,再把图象上每个点的横坐标缩小为原来的一半,得到g(x),则g(x)的解析式为( )
个单位,再把图象上每个点的横坐标缩小为原来的一半,得到g(x),则g(x)的解析式为( )
A.g(x)=sin(4x+ ![]() )
)
B.g(x)=sin(8x﹣ ![]() )??
)??
C.g(x)=sin(x+ ![]() )
)
D.g(x)=sin4x
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=2x2﹣3x+1,g(x)=ksin(x﹣ ![]() )(k≠0).
)(k≠0).
(1)设f(x)的定义域为[0,3],值域为A; g(x)的定义域为[0,3],值域为B,且AB,求实数k的取值范围.
(2)若方程f(sinx)+sinx﹣a=0在[0,2π)上恰有两个解,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=2sin(ωx+φ)(ω>0,0≤φ≤π)的部分图象如图所示,其中A,B两点之间的距离为5,则f(x)的解析式是( ) 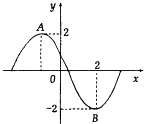
A.y=2sin( ![]() x+
x+ ![]() )
)
B.y=2sin( ![]() x+
x+ ![]() )
)
C.y=2sin( ![]() x+
x+ ![]() )
)
D.y=2sin( ![]() x+
x+ ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为大力提倡“厉行节约,反对浪费”,某市通过随机询问100名性别不同的居民是否能做到“光盘”行动,得到如下的列联表:( )
做不到“光盘” | 能做到“光盘” | |
男 | 45 | 10 |
女 | 30 | 15 |
附:
P(K2 | 0.10 | 0.05 | 0.025 |
k | 2.706 | 3.841 | 5.024 |
![]()
参照附表,得到的正确结论是
A.在犯错误的概率不超过l%的前提下,认为“该市居民能否做到‘光盘’与性别有关”
B.在犯错误的概率不超过l%的前提下,认为“该市居民能否做到‘光盘’与性别无关”
C.有90%以上的把握认为“该市居民能否做到‘光盘’与性别有关”
D.有90%以上的把握认为“该市居民能否做到‘光盘’与性别无关”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的定义域为
的定义域为![]() ,若函数
,若函数![]() 满足:对于给定的
满足:对于给定的![]()
![]() ,存在
,存在![]() ,使得
,使得![]() 成立,那么称
成立,那么称![]() 具有性质
具有性质![]() .
.
(1)函数![]()
![]() 是否具有性质
是否具有性质![]() ?说明理由;
?说明理由;
(2)已知函数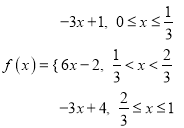 具有性质
具有性质![]() ,求
,求![]() 的最大值;
的最大值;
(3)已知函数![]() 的定义域为
的定义域为![]() ,满足
,满足![]() ,且
,且![]() 的图像是一条连续不断的曲线,问:是否存在正整数n,使得函数
的图像是一条连续不断的曲线,问:是否存在正整数n,使得函数![]() 具有性质
具有性质![]() ,若存在,求出这样的n的取值集合;若不存在,请说明理由.
,若存在,求出这样的n的取值集合;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com