解析:(1)证明:任取x
1<x
2<0,则-x
1>-x
2>0
且f(x)在(0,+∞)上是增函数,
∴f(-x
1)>f(-x
2).又f(x)为奇函数,
故f(x
2)-f(x
1)=-f(-x
2)+f(-x
1)>0
即f(x
1)<f(x
2),f(x)在(-∞,0)上也是增函数.
(2)由g(θ)=sin
2θ+mcosθ-2m=-cos
2θ+mcosθ+1-2m,
令t=cosθ,则0≤t≤1,记y=g(θ)=-t
2+mt+1-2m,由m≤0知,
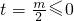
函数y=-t
2+mt+1-2m在t∈[0,1]上是减函数,
故t=0时,g(θ)有最大值1-2m;t=1时,g(θ)有最小值-m.
(3)由f(x)在(-∞,0),(0,+∞)上是增函数,f(-1)=f(1)=0
∵f[g(θ)]<0
∴g(θ)<-1或0<g(θ)<1,又M={m|恒有g(θ)<0},
所以M∩N={m|恒有g(θ)<-1},
即-cos
2θ+mcosθ+1-2m<-1对

恒成立.
∴(2-cosθ)m>2-cos
2θ,
∴
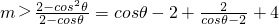
=
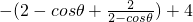
∵

,
∴cosθ-2∈[-2,-1],2-cosθ∈[1,2]
∴
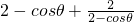
≥2
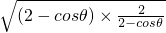
=2

∴
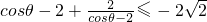
当
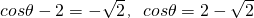
时取得.
∴
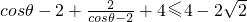
∴
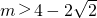
,
故
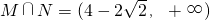
.
分析:(1)任取x
1<x
2<0,则-x
1>-x
2>0,利用单调增函数的定义和奇函数的定义,证明f(x
1)<f(x
2),即可证明f(x)在(-∞,0)上也是增函数;
(2)先将函数g(θ)化为关于cosθ的二次函数,再利用换元法,令t=cosθ,将问题转化为求二次函数在闭区间上的最值问题,最后利用配方法求最值即可;
(3)先将求两集合交集问题转化为一个恒成立问题,即M∩N={m|恒有g(θ)<-1},再利用参变分离法,转化为求函数
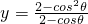
的最大值问题,利用均值定理求其最值即可得m的范围
点评:本题综合考查了函数单调性的定义、函数奇偶性的定义及其二者的综合运用,换元法求三角函数的最值,配方法求二次函数的最值,以及不等式恒成立问题的解法,均值定理的应用,转化化归的思想方法

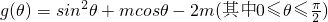
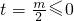
 恒成立.
恒成立.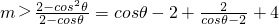 =
=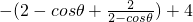
 ,
,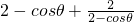 ≥2
≥2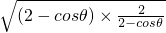 =2
=2
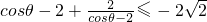
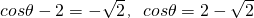 时取得.
时取得.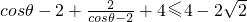
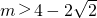 ,
,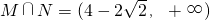 .
.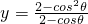 的最大值问题,利用均值定理求其最值即可得m的范围
的最大值问题,利用均值定理求其最值即可得m的范围

