Question

19．在平行四边形形ABCD中，已知AB=8，AD=6，∠BAD=$\frac{2π}{3}$，点E，F分别在边BC，DC上，且BC=3BE，DC=λDF，$\overrightarrow{AE}$•$\overrightarrow{AF}$=16，则λ的值为2．

Answer 1

分析 运用向量的数量积求得$\overrightarrow{AB}$•$\overrightarrow{AD}$，由题意画出图形，把$\overrightarrow{AE}$，$\overrightarrow{AF}$都用含有$\overrightarrow{AB}$，$\overrightarrow{AD}$的式子表示，运用条件$\overrightarrow{AE}$•$\overrightarrow{AF}$=16，展开后化为关于λ的方程，解方程即可得到所求值．

解答 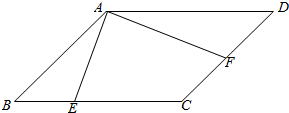解：$\overrightarrow{AB}$•$\overrightarrow{AD}$=|$\overrightarrow{AB}$|•|$\overrightarrow{AD}$|•cos$\frac{2π}{3}$
=8•6•（-$\frac{1}{2}$）=-24，
$\overrightarrow{AE}$•$\overrightarrow{AF}$=（$\overrightarrow{AB}$+$\overrightarrow{BE}$）•（$\overrightarrow{AD}$+$\overrightarrow{DF}$）
=（$\overrightarrow{AB}$+$\frac{1}{3}$$\overrightarrow{BC}$）•（$\overrightarrow{AD}$+$\frac{1}{λ}$$\overrightarrow{DC}$）
=（$\overrightarrow{AB}$+$\frac{1}{3}$$\overrightarrow{AD}$）•（$\overrightarrow{AD}$+$\frac{1}{λ}$$\overrightarrow{AB}$）
=$\frac{1}{3}$$\overrightarrow{AD}$²+$\frac{1}{λ}$$\overrightarrow{AB}$²+（1+$\frac{1}{3λ}$）$\overrightarrow{AB}$•$\overrightarrow{AD}$
=$\frac{1}{3}$•36+$\frac{1}{λ}$•64+（-24）•（1+$\frac{1}{3λ}$）=16，
解得λ=2，
故答案为：2．

点评 本题考查平面向量的数量积运算，考查了向量加法的三角形法则，体现了数学转化思想方法，是中档题．