
【题目】已知函数![]() ,且
,且![]() 在
在![]() 和
和![]() 处取得极值.
处取得极值.
(1)求函数![]() 的解析式;
的解析式;
(2)设函数![]() ,是否存在实数
,是否存在实数![]() ,使得曲线
,使得曲线![]() 与
与![]() 轴有两个交点,若存在,求出
轴有两个交点,若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() .
.
【解析】试题分析:(1)由f(x)=ax3+bx2-2x在x=1或2处取得极值,可得f'(1)=f'(2)=0,故可得到a、b的方程组,求解即可;
(2)曲线y=g(x)与x轴有两个交点,转化成g(x)=0有两个不同的实数解,然后利用导数研究函数的单调性和极值,然后依题意有g(x)极大值=0或g(x)极小值=0即可求出t的值.
试题解析:(1)![]() ,
,
因为![]() 在
在![]() 和
和![]() 处取得极值,
处取得极值,
所以![]() 和
和![]() 是
是![]() 的两个根,
的两个根,
则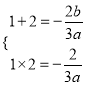 ,解得
,解得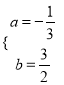 ,
,
经检验符合已知条件,故![]() ;
;
(2)由题意知![]() ,
,
令![]() 得,
得, ![]() 或
或![]() ,
,
![]() 随着
随着![]() 变化情况如下表所示:
变化情况如下表所示:
|
| 1 |
| 2 |
|
| - | 0 | + | 0 | - |
| 递减 | 极小值 | 递增 | 极大值 | 递减 |
由上表可知![]() ,
,
又![]() 取足够大的正数时,
取足够大的正数时, ![]() ,
,
![]() 取足够小的负数时,
取足够小的负数时, ![]() ,
,
因此,为使曲线![]() 与
与![]() 轴有两个交点,结合
轴有两个交点,结合![]() 的单调性,
的单调性,
得![]() 或
或![]() ,
,
∴![]() 或
或![]() ,
,
即存在![]() ,且
,且![]() 或
或![]() 时,曲线
时,曲线![]() 与
与![]() 轴有两个交点.
轴有两个交点.


科目:高中数学 来源: 题型:
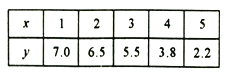
【题目】为了了解某地区某种农产品的年产量![]() (单位:吨)对价格
(单位:吨)对价格![]() (单位:千元/吨)和利润
(单位:千元/吨)和利润![]() 的影响,对近五年该农产品的年产量和价格统计如下表:
的影响,对近五年该农产品的年产量和价格统计如下表:
参考公式: 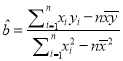 ,
, ![]() .
.
根据参考公式,以求得![]()
(1)求![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)若每吨该农产品的成本为2千元,假设该农产品可全部卖出,预测当年产量为多少时,年利润![]() 取到最大值?(保留两位小数)
取到最大值?(保留两位小数)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某体校为了备战明年四月份省划艇单人双桨比赛,对本校甲、乙两名划艇运动员在相同条件下进行了6次测试,测得他们划艇最大速度![]() 单位:
单位:![]() 数据如下:
数据如下:
甲:27,38,30,37,35,31;
乙:33,29,38,34,28,36.
![]() 试用茎叶图表示甲、乙两名运动员测试的成绩;
试用茎叶图表示甲、乙两名运动员测试的成绩;
![]() 根据测试的成绩,你认为派哪名运动员参加明年四月份的省划艇单人双桨比赛比较合适?并说明你的理由
根据测试的成绩,你认为派哪名运动员参加明年四月份的省划艇单人双桨比赛比较合适?并说明你的理由
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆![]() 的离心率是
的离心率是![]() ,过点
,过点![]() 的动直线
的动直线![]() 与椭圆相交于
与椭圆相交于![]() 两点,当直线
两点,当直线![]() 与
与![]() 轴平行时,直线
轴平行时,直线![]() 被椭圆
被椭圆![]() 截得的线段长为
截得的线段长为![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)在![]() 轴上是否存在异于点
轴上是否存在异于点![]() 的定点
的定点![]() ,使得直线
,使得直线![]() 变化时,总有
变化时,总有![]() ?若存在,求出点
?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四棱锥P﹣ABCD中,PA⊥平面ABCD,底面ABCD是菱形,∠BAD=120°,对角线AC与BD交于点O,M为OC中点. 
(1)求证:BD⊥PM
(2)若二面角O﹣PM﹣D的正切值为2 ![]() ,求
,求 ![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】调查某校 100 名学生的数学成绩情况,得下表:
一般 | 良好 | 优秀 | |
男生(人) |
| 18 |
|
女生(人) | 10 | 17 |
|
已知从这批学生中随机抽取1名学生,抽到成绩一般的男生的概率为0.15.
(1)求![]() 的值;
的值;
(2)若用分层抽样的方法,从这批学生中随机抽取20名,问应在优秀学生中抽多少名?
(3)已知![]() ,优秀学生中男生不少于女生的概率.
,优秀学生中男生不少于女生的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com