
【题目】选修4-4:坐标系与参数方程:
已知极坐标系的极点在直角坐标系的原点,极轴与x轴非负半轴重合,直线l的参数方程为:![]() (t为参数,a∈[0,π),曲线C的极坐标方程为:p=2cosθ.
(t为参数,a∈[0,π),曲线C的极坐标方程为:p=2cosθ.
(Ⅰ)写出曲线C在直角坐标系下的标准方程;
(Ⅱ)设直线l与曲线C相交PQ两点,若|PQ|![]() ,求直线l的斜率.
,求直线l的斜率.
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xoy中,以坐标原点O为极点,x轴正半轴为极轴建立极坐标系。已知曲线C的极坐标方程为![]() ,过点
,过点![]() 的直线l的参数方程为
的直线l的参数方程为 (为参数),直线l与曲线C交于M、N两点。
(为参数),直线l与曲线C交于M、N两点。
(1)写出直线l的普通方程和曲线C的直角坐标方程:
(2)若![]() 成等比数列,求a的值。
成等比数列,求a的值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一场小型晚会有![]() 个唱歌节目和
个唱歌节目和![]() 个相声节目,要求排出一个节目单.
个相声节目,要求排出一个节目单.
(1)![]() 个相声节目要排在一起,有多少种排法?
个相声节目要排在一起,有多少种排法?
(2)![]() 个相声节目彼此要隔开,有多少种排法?
个相声节目彼此要隔开,有多少种排法?
(3)第一个节目和最后一个节目都是唱歌节目,有多少种排法?
(4)前![]() 个节目中要有相声节目,有多少种排法?
个节目中要有相声节目,有多少种排法?
(要求:每小题都要有过程,且计算结果都用数字表示)
查看答案和解析>>
科目:高中数学 来源: 题型:
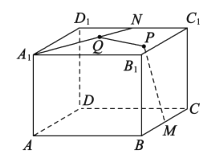
【题目】已知长方体![]() 中,底面ABCD的长AB=4,宽BC=4,高
中,底面ABCD的长AB=4,宽BC=4,高![]() =3,点M,N分别是BC,
=3,点M,N分别是BC,![]() 的中点,点P在上底面
的中点,点P在上底面![]() 中,点Q在
中,点Q在![]() 上,若
上,若![]() ,则PQ长度的最小值是
,则PQ长度的最小值是
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,正四棱椎P-ABCD中,底面ABCD的边长为2,侧棱长为![]() .
.

(I)若点E为PD上的点,且PB∥平面EAC.试确定E点的位置;
(Ⅱ)在(I)的条件下,点F为线段PA上的一点且![]() ,若平面AEC和平面BDF所成的锐二面角的余弦值为
,若平面AEC和平面BDF所成的锐二面角的余弦值为![]() ,求实数
,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解某市高三数学复习备考情况,该市教研机构组织了一次检测考试,并随机抽取了部分高三理科学生数学成绩绘制如图所示的频率分布直方图.

(1)根据频率分布直方图,估计该市此次检测理科数学的平均成绩![]() ;(精确到个位)
;(精确到个位)
(2)研究发现,本次检测的理科数学成绩![]() 近似服从正态分布
近似服从正态分布![]() (
(![]() ,
,![]() 约为
约为![]() ),按以往的统计数据,理科数学成绩能达到自主招生分数要求的同学约占
),按以往的统计数据,理科数学成绩能达到自主招生分数要求的同学约占![]() .
.
(ⅰ)估计本次检测成绩达到自主招生分数要求的理科数学成绩大约是多少分?(精确到个位)
(ⅱ)从该市高三理科学生中随机抽取![]() 人,记理科数学成绩能达到自主招生分数要求的人数为
人,记理科数学成绩能达到自主招生分数要求的人数为![]() ,求
,求![]() 的分布列及数学期望
的分布列及数学期望![]() .(说明:
.(说明:![]() 表示
表示![]() 的概率.参考数据:
的概率.参考数据:![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】改革开放以来,人们的支付方式发生了巨大转变.近年来,移动支付已成为主要支付方式之一.为了解某校学生上个月A,B两种移动支付方式的使用情况,从全校所有的1000名学生中随机抽取了100人,发现样本中A,B两种支付方式都不使用的有5人,样本中仅使用A和仅使用B的学生的支付金额分布情况如下:
支付方式 | 不大于2000元 | 大于2000元 |
仅使用A | 27人 | 3人 |
仅使用B | 24人 | 1人 |
(Ⅰ)估计该校学生中上个月A,B两种支付方式都使用的人数;
(Ⅱ)从样本仅使用B的学生中随机抽取1人,求该学生上个月支付金额大于2000元的概率;
(Ⅲ)已知上个月样本学生的支付方式在本月没有变化.现从样本仅使用B的学生中随机抽查1人,发现他本月的支付金额大于2000元.结合(Ⅱ)的结果,能否认为样本仅使用B的学生中本月支付金额大于2000元的人数有变化?说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com