
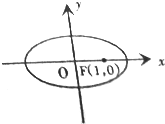
 已知椭圆
已知椭圆| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 3 |
| OC |
| OD |
|
| x2 |
| a2 |
| y2 |
| b2 |
| x2 |
| a2 |
| y2 |
| a2-1 |
| OC |
| OD |
| a2-1 |
| a |
| a2-1 |
| a |
| (a2-1)2 |
| a2 |
|
| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 3 |
|
| x2 |
| 9 |
| y2 |
| 8 |
| x2 |
| a2 |
| y2 |
| b2 |
| x2 |
| a2 |
| y2 |
| a2-1 |
| a2-1 |
| a |
| a2-1 |
| a |
| OC |
| OD |
| a2-1 |
| a |
| a2-1 |
| a |
| (a2-1)2 |
| a2 |
|
| 2a2k2 |
| a2+a2k2-1 |
| a2k2-a4+a2 |
| a2+a2k2-1 |
| OC |
| OD |
| (k2+1)(a2+a2k2-a4)-2k4a2+k2(a2+a2k2-1) |
| a2+a2k2-1 |
| a2-a4-k2(a4-3a2+1) |
| a2(k2+1)-1 |
| 2k2a2+1 |
| 1+k2 |


 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| bnbn+1 |
| 9 |
| 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
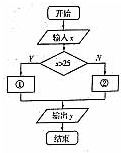 某客运部门规定甲、乙两地之间旅客托运行李的费用为:不超过25kg按0.5元/kg收费,超过25kg的部分按0.8元/kg收费,计算收费的程序框图如右图所示,则①②处应填( )
某客运部门规定甲、乙两地之间旅客托运行李的费用为:不超过25kg按0.5元/kg收费,超过25kg的部分按0.8元/kg收费,计算收费的程序框图如右图所示,则①②处应填( )| A、y=0.8x y=0.5x |
| B、y=0.5x y=0.8x |
| C、y=25×0.5+(x-25)×0.8 y=0.5x |
| D、y=25×0.5+0.8x y=0.8x |
查看答案和解析>>
科目:高中数学 来源: 题型:
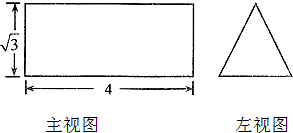 已知正三棱柱ABC-A′B′C′的主视图和侧左视图如图所示.设△ABC的中心分别是O,O′,现将此三棱柱绕直线OO′旋转,在旋转过程中对应的俯视图的面积为S,则S的最大值为( )
已知正三棱柱ABC-A′B′C′的主视图和侧左视图如图所示.设△ABC的中心分别是O,O′,现将此三棱柱绕直线OO′旋转,在旋转过程中对应的俯视图的面积为S,则S的最大值为( )| A、8 | B、4 | C、12 | D、16 |
查看答案和解析>>
科目:高中数学 来源: 题型:
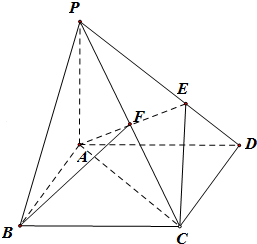 如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠ABC=60°,PA⊥平面ABCD,AP=AB=2,E在PD上,且PE=2ED,F是PC的中点,
如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠ABC=60°,PA⊥平面ABCD,AP=AB=2,E在PD上,且PE=2ED,F是PC的中点,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com