
【题目】在数列![]() 中,
中,![]() ,且对任意
,且对任意![]() ,
,![]() 成等差数列,其公差为
成等差数列,其公差为![]() .
.
(1)若![]() ,求
,求![]() 的值;
的值;
(2)若![]() ,证明
,证明![]() 成等比数列(
成等比数列(![]() );
);
(3)若对任意![]() ,
,![]() 成等比数列,其公比为
成等比数列,其公比为![]() ,设
,设![]() ,证明数列
,证明数列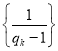 是等差数列.
是等差数列.
科目:高中数学 来源: 题型:
【题目】某口袋内装有一些除颜色不同之外其他均相同的红球、白球和黑球,从中摸出1个球,摸出红球的概率是0.42,摸出白球的概率是0.28,若红球有21个,则黑球有_________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)阅读以下案例,利用此案例的想法化简![]() .
.
案例:考察恒等式![]() 左右两边
左右两边![]() 的系数.
的系数.
因为右边![]() ,
,
所以,右边![]() 的系数为
的系数为![]() ,
,
而左边![]() 的系数为
的系数为![]() ,
,
所以![]() =
=![]() .
.
(2)求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)若曲线![]() 在
在![]() 处的切线的斜率为3,求实数
处的切线的斜率为3,求实数![]() 的值;
的值;
(2)若函数在区间![]() 上存在极小值,求实数
上存在极小值,求实数![]() 的取值范围;
的取值范围;
(3)如果![]() 的解集中只有一个整数,求实数
的解集中只有一个整数,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】过去大多数人采用储蓄的方式将钱储蓄起来,以保证自己生活的稳定,考虑到通货膨胀的压力,如果我们把所有的钱都用来储蓄,这并不是一种很好的方式,随着金融业的发展,普通人能够使用的投资理财工具也多了起来,为了研究某种理财工具的使用情况,现对![]() 年龄段的人员进行了调查研究,将各年龄段人数分成
年龄段的人员进行了调查研究,将各年龄段人数分成![]() 组:
组:![]() ,并整理得到频率分布直方图:
,并整理得到频率分布直方图:
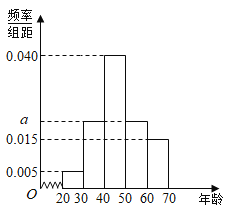
(1)求图中的![]() 值;
值;
(2)采用分层抽样的方法,从第二组、第三组、第四组中共抽取![]() 人,则三个组中各抽取多少人?
人,则三个组中各抽取多少人?
(3)在(2)中抽取的![]() 人中,随机抽取
人中,随机抽取![]() 人,则这
人,则这![]() 人都来自于第三组的概率是多少?
人都来自于第三组的概率是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年4月,甲乙两校的学生参加了某考试机构举行的大联考,现对这两校参加考试的学生的数学成绩进行统计分析,数据统计显示,考生的数学成绩![]() 服从正态分布
服从正态分布![]() ,从甲乙两校100分及以上的试卷中用系统抽样的方法各抽取了20份试卷,并将这40份试卷的得分制作成如图所示的茎叶图:
,从甲乙两校100分及以上的试卷中用系统抽样的方法各抽取了20份试卷,并将这40份试卷的得分制作成如图所示的茎叶图:
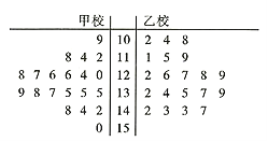
(1)试通过茎叶图比较这40份试卷的两校学生数学成绩的中位数;
(2)若把数学成绩不低于135分的记作数学成绩优秀,根据茎叶图中的数据,判断是否有![]() 的把握认为数学成绩在100分及以上的学生中数学成绩是否优秀与所在学校有关?
的把握认为数学成绩在100分及以上的学生中数学成绩是否优秀与所在学校有关?
(3)从所有参加此次联考的学生中(人数很多)任意抽取3人,记数学成绩在134分以上的人数为![]() ,求
,求![]() 的数学期望.
的数学期望.
附:若随机变量![]() 服从正态分布
服从正态分布![]() ,则
,则![]() ,
,![]()
![]() ,
,![]() .
.
参考公式与临界值表:![]() ,其中
,其中![]() .
.
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知直线
中,已知直线![]() 的方程为
的方程为![]() ,曲线
,曲线![]() 是以坐标原点
是以坐标原点![]() 为顶点,直线
为顶点,直线![]() 为准线的抛物线.以坐标原点
为准线的抛物线.以坐标原点![]() 为极点,
为极点,![]() 轴非负半轴为极轴建立极坐标系.
轴非负半轴为极轴建立极坐标系.
(1)分别求出直线![]() 与曲线
与曲线![]() 的极坐标方程:
的极坐标方程:
(2)点![]() 是曲线
是曲线![]() 上位于第一象限内的一个动点,点
上位于第一象限内的一个动点,点![]() 是直线
是直线![]() 上位于第二象限内的一个动点,且
上位于第二象限内的一个动点,且![]() ,请求出
,请求出![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com