
【题目】数列{an}中,a1=1,an﹣an+1=anan+1 , n∈N* .
(1)求数列{an}的通项公式;
(2)Sn为{an}的前n项和,bn=S2n﹣Sn , 求bn的最小值.
【答案】
(1)解:∵a1=1,an﹣an+1=anan+1,n∈N*.∴ ![]() =1,
=1,
∴数列 ![]() 是等差数列,公差为1,首项为1.
是等差数列,公差为1,首项为1.
∴ ![]() =1+(n﹣1)=n,可得an=
=1+(n﹣1)=n,可得an= ![]()
(2)解:由(1)可得:Sn=1+ ![]() +…+
+…+ ![]() .
.
∴bn=S2n﹣Sn= ![]() +…+
+…+ ![]() .
.
∴bn+1﹣bn= ![]() +…+
+…+ ![]() +
+ ![]() +
+ ![]() ﹣(
﹣( ![]() +…+
+…+ ![]() )
)
= ![]() +
+ ![]() ﹣
﹣ ![]() =
= ![]() ﹣
﹣ ![]() >0,
>0,
∴数列{bn}单调递增,∴bn的最小值为b1= ![]()
【解析】(1)由a1=1,an﹣an+1=anan+1 , n∈N* . 可得 ![]() =1,利用等差数列的通项公式即可得出.(2)由(1)可得:bn=S2n﹣Sn=
=1,利用等差数列的通项公式即可得出.(2)由(1)可得:bn=S2n﹣Sn= ![]() +…+
+…+ ![]() .再利用数列的单调性即可得出.
.再利用数列的单调性即可得出.
【考点精析】本题主要考查了数列的前n项和和数列的通项公式的相关知识点,需要掌握数列{an}的前n项和sn与通项an的关系 ;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式才能正确解答此题.
;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】如图,已知四棱锥P﹣ABCD的底面为菱形,∠BCD=120°,AB=PC=2,AP=BP= ![]() .
. 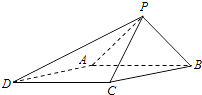
(1)求证:AB⊥PC;
(2)求二面角B一PC﹣D的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正方体ABCD-A1B1C1D1中,M,N,P分别是C1C, C1B1,C1D1的中点,点H在四边形A1ADD1的边及其内部运动,则H满足条件________时,有BH∥平面MNP.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某园林基地培育了一种新观赏植物,经过一年的生长发育,技术人员从中抽取了部分植株的高度(单位:厘米)作为样本(样本容量为![]() )进行统计,按照
)进行统计,按照![]()
![]() 的分组作出频率分布直方图,并作出样本高度的茎叶图(图中仅列出了高度在
的分组作出频率分布直方图,并作出样本高度的茎叶图(图中仅列出了高度在![]() 的数据).
的数据).
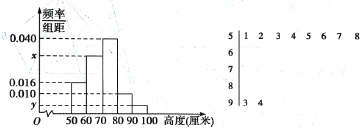
(1)求样本容量![]() 和频率分布直方图中的
和频率分布直方图中的![]() 的值;
的值;
(2)在选取的样本中,从高度在![]() 厘米以上(含
厘米以上(含![]() 厘米)的植株中随机抽取
厘米)的植株中随机抽取![]() 株,求所取的
株,求所取的![]() 株中至少有一株高度在
株中至少有一株高度在![]() 内的概率.
内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆E的中心在原点,焦点在x轴上,椭圆的左顶点坐标为![]() ,离心率为
,离心率为![]() .
.
![]() 求椭圆E的方程;
求椭圆E的方程;
![]() 过点
过点![]() 作直线l交E于P、Q两点,试问:在x轴上是否存在一个定点M,使
作直线l交E于P、Q两点,试问:在x轴上是否存在一个定点M,使![]() 为定值?若存在,求出这个定点M的坐标;若不存在,请说明理由.
为定值?若存在,求出这个定点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法中错误的序号是: _________
①已知![]() 恒成立,若
恒成立,若![]() 为真命题,则实数
为真命题,则实数![]() 的最大值为2;
的最大值为2;
②已知三点![]() 共线,则
共线,则![]() 的最小值为11;
的最小值为11;
③已知![]() 是椭圆
是椭圆![]() 的为两个焦点,点
的为两个焦点,点![]() 在椭圆
在椭圆![]() 上,则使三角形
上,则使三角形![]() 为直角三角形的点
为直角三角形的点![]() 个数4 个;
个数4 个;
④在圆![]() 内,过点
内,过点![]() 有
有![]() 条弦的长度成等差数列,最小弦长为数列的首项
条弦的长度成等差数列,最小弦长为数列的首项![]() ,最大弦长为
,最大弦长为![]() ,若公差
,若公差![]() 那么
那么![]() 的取值集合为
的取值集合为![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆C:![]() +
+![]() =1(a>b>0)的短轴两端点为B1(0,﹣1)、B2(0,1),离心率e=
=1(a>b>0)的短轴两端点为B1(0,﹣1)、B2(0,1),离心率e=![]() ,点P是椭圆C上不在坐标轴上的任意一点,直线B1P和B2P分别与x轴相交于M,N两点,
,点P是椭圆C上不在坐标轴上的任意一点,直线B1P和B2P分别与x轴相交于M,N两点,

(1)求椭圆![]() 的方程和
的方程和![]() 的值;
的值;
(2)若点![]() 坐标为(1,0),过
坐标为(1,0),过![]() 点的直线
点的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点,试求
两点,试求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com