
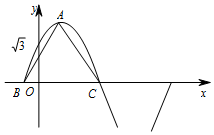
 已知函数$f(x)=Asin({ωx+φ})({A>0\;,\;\;ω>0\;,\;\;|φ|<\frac{π}{2}})$在一个周期内的图象如图所示,图象过点$({0\;,\;\;\sqrt{3}})$,A为图象的最高点,B,C为图象与x轴的交点,且△ABC为高为$2\sqrt{3}$的正三角形.
已知函数$f(x)=Asin({ωx+φ})({A>0\;,\;\;ω>0\;,\;\;|φ|<\frac{π}{2}})$在一个周期内的图象如图所示,图象过点$({0\;,\;\;\sqrt{3}})$,A为图象的最高点,B,C为图象与x轴的交点,且△ABC为高为$2\sqrt{3}$的正三角形.分析 (1)根据三角函数的图象,结合三角函数的性质即可求A,ω和φ的值,
(2)根据三角函数的解析式,求出角的范围即可求出函数的值域,
(3)利用三角函数的图象平移关系求出g(x)的解析式,结合函数的对称性进行求解即可.
解答 解:(1)∵△ABC为高为$2\sqrt{3}$的正三角形,
∴A=2$\sqrt{3}$,
则sin60°=$\frac{2\sqrt{3}}{AB}$=$\frac{\sqrt{3}}{2}$,则AB=BC=4,
即函数的周期T=2BC=8=$\frac{2π}{ω}$,
则ω=$\frac{π}{4}$,
此时f(x)=2$\sqrt{3}$sin($\frac{π}{4}$x+φ),
∵图象过点$({0\;,\;\;\sqrt{3}})$,
∴f(0)=2$\sqrt{3}$sinφ=$\sqrt{3}$,
则sinφ=$\frac{1}{2}$,
∵|φ|<$\frac{π}{2}$,∴φ=$\frac{π}{6}$,
即A=2$\sqrt{3}$,ω=$\frac{π}{4}$,φ=$\frac{π}{6}$;
(2)由(1)得f(x)=2$\sqrt{3}$sin($\frac{π}{4}$x+$\frac{π}{6}$),
当$x∈[{-\frac{2}{3}\;,\;\;\frac{4}{3}}]$时,
即-$\frac{2}{3}$≤x≤$\frac{4}{3}$,
则0≤$\frac{π}{4}$x+$\frac{π}{6}$≤$\frac{π}{2}$,
∴当$\frac{π}{4}$x+$\frac{π}{6}$=$\frac{π}{2}$时,函数取得最大值为2$\sqrt{3}$,
当$\frac{π}{4}$x+$\frac{π}{6}$=0时,函数取得最小值为0,
即函数f(x)的值域为[0,2$\sqrt{3}$];
(3)将y=f(x)的图象所在点向左平行移动θ(θ>0)的单位长度,得到y=g(x)的图象.
即g(x)=2$\sqrt{3}$sin[$\frac{π}{4}$(x+θ)+$\frac{π}{6}$]=2$\sqrt{3}$sin($\frac{π}{4}$x+$\frac{π}{4}$θ+$\frac{π}{6}$),
若y=g(x)的图象的一个对称中心为$({\frac{2}{3}\;,\;\;0})$,
即$\frac{π}{4}$×$\frac{2}{3}$+$\frac{π}{4}$θ+$\frac{π}{6}$=kπ,k∈Z
则θ=4k-$\frac{4}{3}$,k∈Z.
∵θ>0,∴当k=1时,θ取得最小值此时θ的最小值为4-$\frac{4}{3}$=$\frac{8}{3}$.
点评 本题主要考查三角函数的图象和性质,利用图象求出函数的解析式是解决本题的关键.综合性较强,运算量较大.


 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 本学期王老师任教两个平行班高三A班、高三B班,两个班都是50个学生,如图图反映的是两个班在本学期5次数学测试中的班级平均分对比,根据图表,不正确的结论是( )
本学期王老师任教两个平行班高三A班、高三B班,两个班都是50个学生,如图图反映的是两个班在本学期5次数学测试中的班级平均分对比,根据图表,不正确的结论是( )| A. | A班的数学成绩平均水平好于B班 | |
| B. | B班的数学成绩没有A班稳定 | |
| C. | 下次考试B班的数学平均分要高于A班 | |
| D. | 在第1次考试中,A、B两个班的总平均分为98 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com