
【题目】已知函数![]() .
.
(![]() )当
)当![]() 时,求
时,求![]() 在区间
在区间![]() 上的取值范围.
上的取值范围.
(![]() )当
)当![]() 时,
时,![]() ,求
,求![]() 的值.
的值.
【答案】(1)当m=0时,![]()
![]() ,由已知
,由已知![]() ,得
,得![]()
从而得:![]() 的值域为
的值域为![]()
(2)![]()
化简得:![]()
当![]() ,得:
,得:![]() ,
,![]() ,
,
代入上式,m=-2.
【解析】
试题(1)把m=0代入到f(x)中,然后分别利用同角三角函数间的基本关系、二倍角的正弦、余弦函数公式以及特殊角的三角函数值把f(x)化为一个角的正弦函数,利用x的范围求出此正弦函数角的范围,根据角的范围,利用正弦函数的图象即可得到f(x)的值域;
(2)把f(x)的解析式利用二倍角的正弦、余弦函数公式及积化和差公式化简得到关于sin2x和cos2x的式子,把x换成α,根据tanα的值,利用同角三角函数间的基本关系以及二倍角的正弦函数公式化简求出sin2α和cos2α的值,把sin2α和cos2α的值代入到f(α)=![]() 中得到关于m的方程,求出m的值即可.
中得到关于m的方程,求出m的值即可.
试题解析:(1)当m=0时,f(x)=(1+![]() )sin2x=sin2x+sinxcosx=
)sin2x=sin2x+sinxcosx=![]() ,由已知
,由已知![]() ,得
,得![]() ,从而得
,从而得![]() 的值域为[0,
的值域为[0,![]() ].
].
由f(x)=(1+![]() )sin2x+msin(x+
)sin2x+msin(x+![]() )sin(x-
)sin(x-![]() )
)
![]() ,所以
,所以![]() ,当
,当![]() ,得
,得![]() ,
,![]() ,代入式得
,代入式得![]()


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图,在圆心角为![]() ,半径为
,半径为![]() 的扇形铁皮上截取一块矩形材料
的扇形铁皮上截取一块矩形材料![]() ,其中点
,其中点![]() 为圆心,点
为圆心,点![]() 在圆弧上,点
在圆弧上,点![]() 在两半径上,现将此矩形铁皮
在两半径上,现将此矩形铁皮![]() 卷成一个以
卷成一个以![]() 为母线的圆柱形铁皮罐的侧面(不计剪裁和拼接损耗),设矩形的边长
为母线的圆柱形铁皮罐的侧面(不计剪裁和拼接损耗),设矩形的边长![]() ,圆柱形铁皮罐的容积为
,圆柱形铁皮罐的容积为![]() .
.

(1)求圆柱形铁皮罐的容积![]() 关于
关于![]() 的函数解析式,并指出该函数的定义域;
的函数解析式,并指出该函数的定义域;
(2)当![]() 为何值时,才使做出的圆柱形铁皮罐的容积
为何值时,才使做出的圆柱形铁皮罐的容积![]() 最大?最大容积是多少? (圆柱体积公式:
最大?最大容积是多少? (圆柱体积公式:![]() ,
,![]() 为圆柱的底面枳,
为圆柱的底面枳,![]() 为圆柱的高)
为圆柱的高)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A.“sinα= ![]() ”是“cos2α=
”是“cos2α= ![]() ”的必要不充分条件
”的必要不充分条件
B.已知命题p:?x∈R,使2x>3x;命题q:?x∈(0,+∞),都有 ![]() <
< ![]() ,则p∧(¬q)是真命题
,则p∧(¬q)是真命题
C.命题“若xy=0,则x=0或y=0”的否命题是“若xy≠0,则x≠0或y≠0”
D.从匀速传递的生产流水线上,质检员每隔5分钟从中抽取一件产品进行某项指标检测,这是分成抽样
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)= ![]() sinxcosx+cos2x,锐角△ABC的三个角A,B,C所对的边分别为a,b,c. (Ⅰ)求函数f(x)的最小正周期和单调递增区间;
sinxcosx+cos2x,锐角△ABC的三个角A,B,C所对的边分别为a,b,c. (Ⅰ)求函数f(x)的最小正周期和单调递增区间;
(Ⅱ)若f(C)=1,求m= ![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,C是圆周上不同于A,B的任意一点,PA⊥平面ABC,则四面体P-ABC的四个面中,直角三角形的个数有( )
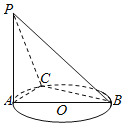
A. 4个B. 3个C. 2个D. 1个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C的对边分别为a,b,c,且满足(2a-b)cosC-ccosB=0.
(Ⅰ)求角C的值;
(Ⅱ)若三边a,b,c满足a+b=13,c=7,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆![]() 一个焦点为
一个焦点为![]() ,离心率
,离心率![]() .
.
(Ⅰ)求椭圆![]() 的方程式.
的方程式.
(Ⅱ)定点![]() ,
,![]() 为椭圆
为椭圆![]() 上的动点,求
上的动点,求![]() 的最大值;并求出取最大值时
的最大值;并求出取最大值时![]() 点的坐标求.
点的坐标求.
(Ⅲ)定直线![]() ,
,![]() 为椭圆
为椭圆![]() 上的动点,证明点
上的动点,证明点![]() 到
到![]() 的距离与到定直线
的距离与到定直线![]() 的距离的比值为常数,并求出此常数值.
的距离的比值为常数,并求出此常数值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com