
【题目】已知函数![]() ,
,![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的单调区间;
的单调区间;
(2)设函数![]() ,
,![]() .若函数
.若函数![]() 的最小值是
的最小值是![]() ,求
,求![]() 的值;
的值;
(3)若函数![]() ,
,![]() 的定义域都是
的定义域都是![]() ,对于函数
,对于函数![]() 的图象上的任意一点
的图象上的任意一点![]() ,在函数
,在函数![]() 的图象上都存在一点
的图象上都存在一点![]() ,使得
,使得![]() ,其中
,其中![]() 是自然对数的底数,
是自然对数的底数,![]() 为坐标原点,求
为坐标原点,求![]() 的取值范围.
的取值范围.
【答案】(1)见解析(2)1(3)![]()
【解析】试题分析:
(1) 当![]() 时,
时,![]() ,可得函数
,可得函数![]() 的单调增区间是
的单调增区间是![]() ,单调减区间为
,单调减区间为![]() ;
;
(2) ![]() ,令
,令![]() 得
得![]() ,
,
函数![]() 在
在![]() 上单调减;函数
上单调减;函数![]() 在
在![]() 上单调增.
上单调增.
所以![]() .分类讨论:
.分类讨论:
①当![]() 时,
时,![]() ;
;
②当![]() 时,解得
时,解得![]() (舍).
(舍).
综上所述,![]() 的值为1.
的值为1.
(3)由题意可知函数![]() 在
在![]() 上单调增,故
上单调增,故![]() .
.
所以![]() ,即
,即![]() 在
在![]() 上恒成立,
上恒成立,
构造函数:设![]() ,设
,设![]() ,结合函数的性质可得,
,结合函数的性质可得,![]() 的取值范围为
的取值范围为![]() .
.
试题解析:
解:(1) 当![]() 时,
时,![]() ,
,![]() .
.
因为![]() 在
在![]() 上单调增,且
上单调增,且![]() ,
,
所以当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
所以函数![]() 的单调增区间是
的单调增区间是![]() .
.
(2)![]() ,则
,则![]() ,令
,令![]() 得
得![]() ,
,
当![]() 时,
时,![]() ,函数
,函数![]() 在
在![]() 上单调减;
上单调减;
当![]() 时,
时,![]() ,函数
,函数![]() 在
在![]() 上单调增.
上单调增.
所以![]() .
.
①当![]() ,即
,即![]() 时,
时,
函数![]() 的最小值
的最小值![]()
![]() ,
,
即![]() ,解得
,解得![]() 或
或![]() (舍),所以
(舍),所以![]() ;
;
②当![]() ,即
,即![]() 时,
时,
函数![]() 的最小值
的最小值![]() ,解得
,解得![]() (舍).
(舍).
综上所述,![]() 的值为1.
的值为1.
(3)由题意知,![]() ,
,![]() .
.
考虑函数![]() ,因为
,因为![]() 在
在![]() 上恒成立,
上恒成立,
所以函数![]() 在
在![]() 上单调增,故
上单调增,故![]() .
.
所以![]() ,即
,即![]() 在
在![]() 上恒成立,
上恒成立,
即![]() 在
在![]() 上恒成立.
上恒成立.
设![]() ,则
,则![]() 在
在![]() 上恒成立,
上恒成立,
所以![]() 在
在![]() 上单调减,所以
上单调减,所以![]() .
.
设![]() ,
,
则![]()
![]() 在
在![]() 上恒成立,
上恒成立,
所以![]() 在
在![]() 上单调增,所以
上单调增,所以![]() .
.
综上所述,![]() 的取值范围为
的取值范围为![]() .
.


科目:高中数学 来源: 题型:
【题目】如图,经过点![]() 作两条互相垂直的直线
作两条互相垂直的直线![]() 和
和![]() ,直线
,直线![]() 交
交![]() 轴正半轴于点
轴正半轴于点![]() ,直线
,直线![]() 交
交![]() 轴正半轴于点
轴正半轴于点![]() .
.
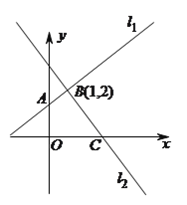
(1)如果![]() ,求点
,求点![]() 的坐标.
的坐标.
(2)试问是否总存在经过![]() ,
, ![]() ,
, ![]() ,
, ![]() 四点的圆?如果存在,求出半径最小的圆的方程;如果不存在,请说明理由.
四点的圆?如果存在,求出半径最小的圆的方程;如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足a1=1,an= ![]() (n∈N* , n≥2),数列{bn}满足关系式bn=
(n∈N* , n≥2),数列{bn}满足关系式bn= ![]() (n∈N*).
(n∈N*).
(1)求证:数列{bn}为等差数列;
(2)求数列{an}的通项公式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两个粮库要向A,B两镇运送大米,已知甲库可调出100 t大米,乙库可调出80 t大米,A镇需70 t大米,B镇需110 t大米.两库到两镇的路程和运费如下表:

这两个粮库各运往A,B两镇多少t大米,才能使总运费最省?此时总运费是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l1经过点A(﹣3,0),B(3,2),直线l2经过点B,且l1⊥l2 .
(1)求经过点B且在两坐标轴上的截距相等的直线的方程;
(2)设直线l2与直线y=8x的交点为C,求△ABC外接圆的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}是首项为a1= ![]() ,公比q=
,公比q= ![]() 的等比数列,设bn+2=3
的等比数列,设bn+2=3 ![]() an(n∈N*),数列{cn}满足cn=anbn .
an(n∈N*),数列{cn}满足cn=anbn .
(1)求证:{bn}是等差数列;
(2)求数列{cn}的前n项和Sn;
(3)若cn≤ ![]() +m﹣1对一切正整数n恒成立,求实数m的取值范围.
+m﹣1对一切正整数n恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了丰富退休生活,老王坚持每天健步走,并用计步器记录每天健步走的步数.他从某月中随机抽取20天的健步走步数(老王每天健步走的步数都在![]() 之间,单位:千步),绘制出频率分布直方图(不完整)如图所示.
之间,单位:千步),绘制出频率分布直方图(不完整)如图所示.
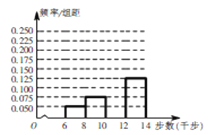
(1)完成频率分布直方图,并估计该月老王每天健步走的平均步数(每组数据可用区间中点值代替;
(2)某健康组织对健步走步数的评价标准如下表:
每天步数分组(千步) |
|
|
|
评价级别 | 及格 | 良好 | 优秀 |
现从这20天中评价级别是“及格”或“良好”的天数里随机抽取2天,求这2天的健步走结果属于同一评价级别的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】假定小麦基本苗数x与成熟期有效穗y之间存在相关关系,今测得5组数据如下:
x | 15.0 | 25.58 | 30.0 | 36.6 | 44.4 |
y | 39.4 | 42.9 | 42.9 | 43.1 | 49.2 |
(1)以x为解释变量,y为预报变量,作出散点图;
(2)求y与x之间的线性回归方程,对于基本苗数56.7预报其有效穗;
(3)计算各组残差,并计算残差平方和;
(4)求R2,并说明残差变量对有效穗的影响占百分之几.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com