
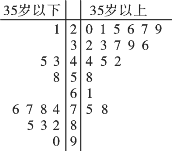
【题目】某单位对其![]() 名员工的饮食习惯进行了一次调查,并用如图所示的茎叶图表示他们的饮食指数(说明:图中饮食指数低于
名员工的饮食习惯进行了一次调查,并用如图所示的茎叶图表示他们的饮食指数(说明:图中饮食指数低于![]() 的人,喜食蔬菜;饮食指数高于
的人,喜食蔬菜;饮食指数高于![]() 的人,喜食肉类).
的人,喜食肉类).
(1)根据所给数据完成下面的![]() 列联表;
列联表;
喜食蔬菜 | 喜食肉类 | 总计 | |
35岁以上 | |||
35岁以下 | |||
总计 |
(2)能否有![]() 的把握认为该单位员工的饮食习惯与年龄有关?
的把握认为该单位员工的饮食习惯与年龄有关?
独立性检验的临界值表:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
参考公式: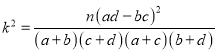 ,
,![]() .
.
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P-ABCD中,侧面PAD是边长为2的等边三角形且垂直于底![]() ,
, ![]()
![]() 是
是![]() 的中点。
的中点。
(1)证明:直线![]() 平面
平面![]() ;
;
(2)点![]() 在棱
在棱![]() 上,且直线
上,且直线![]() 与底面
与底面![]() 所成角为
所成角为![]() ,求二面角
,求二面角![]() 的余弦值。
的余弦值。

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了庆祝第一个农民丰收节,西部山区某村统计了自2011年以来每年的年总收入,其中2018年统计的是1月到8月的总收入,统计结果如图所示.根据图形,下列四个判断中,错误的是( )
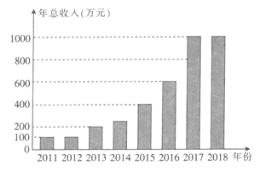
A.从2012年起,年总收入逐年增加B.2017年的年总收入在2016年的基础上翻了番
C.年份数与年总收入成正相关D.由图可预测从2014年起年总收入增长加快
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,已知点A(5,-2),B(7,3),且边AC的中点M在y轴上,边BC的中点N在x轴上,求:
(1)顶点C的坐标;
(2)直线MN的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() ,焦点为
,焦点为![]() ,直线
,直线![]() 交抛物线
交抛物线![]() 于
于![]() 两点,
两点,![]() 是线段
是线段![]() 的中点,过
的中点,过![]() 作
作![]() 轴的垂线交抛物线
轴的垂线交抛物线![]() 于点
于点![]() .
.
(1)求抛物线![]() 的焦点坐标;
的焦点坐标;
(2)若抛物线![]() 上有一点
上有一点![]() 到焦点
到焦点![]() 的距离为
的距离为![]() ,求此时
,求此时![]() 的值;
的值;
(3)是否存在实数![]() ,使
,使![]() 是以
是以![]() 为直角顶点的直角三角形?若存在,求出
为直角顶点的直角三角形?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在矩形![]() 中,
中,![]() ,
,![]() .将矩形
.将矩形![]() 沿对角线
沿对角线![]() 翻折形成四面体
翻折形成四面体![]() ,若该四面体
,若该四面体![]() 内接于球
内接于球![]() ,则下列说法错误的是( )
,则下列说法错误的是( )
A.四面体![]() 的体积的最大值是
的体积的最大值是![]() B.球心
B.球心![]() 为线段
为线段![]() 的中点
的中点
C.球![]() 的表面积随二面角
的表面积随二面角![]() 的变化而变化D.球
的变化而变化D.球![]() 的表面积为定值
的表面积为定值![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,随着互联网的发展,诸如“滴滴打车”“神州专车”等网约车服务在我国各:城市迅猛发展,为人们出行提供了便利,但也给城市交通管理带来了一些困难.为掌握网约车在![]() 省的发展情况,
省的发展情况,![]() 省某调查机构从该省抽取了
省某调查机构从该省抽取了![]() 个城市,分别收集和分析了网约车的
个城市,分别收集和分析了网约车的![]() 两项指标数
两项指标数![]() ,数据如下表所示:
,数据如下表所示:
城市1 | 城市2 | 城市3 | 城市4 | 城市5 | |
|
|
|
|
|
|
|
|
|
|
|
|
经计算得: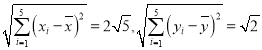
(1)试求![]() 与
与![]() 间的相关系数
间的相关系数![]() ,并利用
,并利用![]() 说明
说明![]() 与
与![]() 是否具有较强的线性相关关系(若
是否具有较强的线性相关关系(若![]() ,则线性相关程度很高,可用线性回归模型拟合);
,则线性相关程度很高,可用线性回归模型拟合);
(2)立![]() 关于
关于![]() 的回归方程,并预测当
的回归方程,并预测当![]() 指标数为
指标数为![]() 时,
时,![]() 指标数的估计值.
指标数的估计值.
附:相关公式: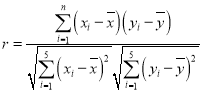 ,
,
参考数据:![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com