
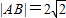 ,求直线l的方程;
,求直线l的方程;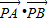 ,并求
,并求 的取值范围.
的取值范围.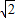 的双曲线,由此可得动圆圆心P的轨迹E的方程;
的双曲线,由此可得动圆圆心P的轨迹E的方程;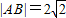 ,可求直线l的方程;
,可求直线l的方程;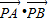 ,利用函数的单调性,即可求
,利用函数的单调性,即可求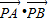 的取值范围.
的取值范围.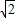 ,∴点P的轨迹是以M(-2,0),N(2,0)为焦点,实轴长为2
,∴点P的轨迹是以M(-2,0),N(2,0)为焦点,实轴长为2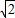 的双曲线.
的双曲线.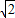 ,c=2,∴b=
,c=2,∴b=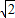
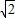 ),B(2,-
),B(2,- ),|AB|=2
),|AB|=2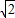 满足题意;
满足题意;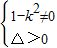 ,可得k≠±1
,可得k≠±1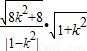 =2
=2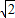 ,∴k=0即l:y=0
,∴k=0即l:y=0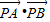 =
=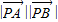 cos∠APB=(t2-1)(1-2sin2APC)=(t2-1)[1-2(
cos∠APB=(t2-1)(1-2sin2APC)=(t2-1)[1-2( )2]=
)2]=
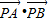 =
=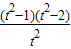 =
=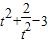
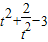 在[
在[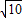 ,+∞)是增函数,
,+∞)是增函数,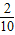 -3=7
-3=7
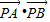 的取值范围是[7
的取值范围是[7 ,+∞).
,+∞).

科目:高中数学 来源: 题型:
| 2 |
| PA |
| PB |
| PA |
| PB |
查看答案和解析>>
科目:高中数学 来源: 题型:
2
| ||
| 3 |
2
| ||
| 3 |
| OA |
| OB |
| OD |
| OE |
| OF |
| TE |
| TF |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:2011-2012学年湖南师大附中高三第三次月考数学试卷(理科)(解析版) 题型:解答题
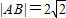 ,求直线l的方程;
,求直线l的方程;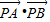 ,并求
,并求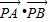 的取值范围.
的取值范围.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com