
【题目】已知双曲线![]() =1,P为双曲线右支上除x轴上之外的一点.
=1,P为双曲线右支上除x轴上之外的一点.
(1)若∠F1PF2=θ,求△F1PF2的面积.
(2)若该双曲线与椭圆![]() +y2=1有共同的焦点且过点A(2,1),求△F1PF2内切圆的圆心轨迹方程.
+y2=1有共同的焦点且过点A(2,1),求△F1PF2内切圆的圆心轨迹方程.
【答案】(1) b2![]() (2) x=
(2) x=![]() (y≠0).
(y≠0).
【解析】
(1)设|PF1|=m,|PF2|=n,运用双曲线的定义和余弦定理,三角形的面积公式,化简可得所求面积;
(2)由内切圆的切线的性质和双曲线的定义,化简可得内心的横坐标为a,求得双曲线的方程,可得所求轨迹方程.
解:(1)∠F1PF2=θ,设|PF1|=m,|PF2|=n,
由双曲线的定义可得m-n=2a,
4c2=m2+n2-2mncosθ=(m-n)2+2mn-2mncosθ=4a2+2mn(1-cosθ),
可得mn=![]() ,
,
则△F1PF2的面积为S=![]() mnsinθ=b2
mnsinθ=b2![]() =b2
=b2![]() ;
;
(2)如图所示:F1(-c,0)、F2(c,0),
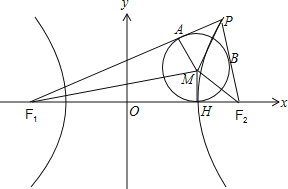
设内切圆与x轴的切点是点H,
PF1、PF2与内切圆的切点分别为A、B,
由双曲线的定义可得|PF1|-|PF2|=2a,
由圆的切线长定理知,|PA|=|PB|,
故|AF1|-|BF2|=2a,
即|HF1|-|HF2|=2a,
设内切圆的圆心横坐标为x,则点H的横坐标为x,
故(x +c)-(c-x)=2a,
∴x=a;
该双曲线与椭圆![]() +y2=1有共同的焦点(±
+y2=1有共同的焦点(±![]() ,0),
,0),
且过点A(2,1),可得a2+b2=3,![]() -
-![]() =1,
=1,
解得a=![]() ,b=1,
,b=1,
可得△F1PF2内切圆的圆心轨迹方程为x=![]() (y≠0).
(y≠0).


 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】为了解某校学生参加社区服务的情况,采用按性别分层抽样的方法进行调查.已知该校共有学生960人,其中男生560人,从全校学生中抽取了容量为![]() 的样本,得到一周参加社区服务的时间的统计数据如下表:
的样本,得到一周参加社区服务的时间的统计数据如下表:
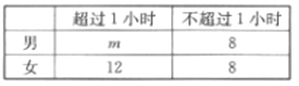
(1)求![]() ,
,![]() ;
;
(2)能否有![]() 的把握认为该校学生一周参加社区服务时间是否超过1小时与性别有关?
的把握认为该校学生一周参加社区服务时间是否超过1小时与性别有关?
附:
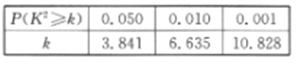
![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某校有歌唱和舞蹈两个兴趣小组,其中歌唱组有 4 名男生,1 名女生,舞蹈组有2 名男生,2 名女生,学校计划从两兴趣小组中各选2名同学参加演出.
(1)求选出的4名同学中至多有2名女生的选派方法数;
(2)记X为选出的4名同学中女生的人数,求X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() 的左右焦点分别为F1,F2,点P 在椭圆上运动,
的左右焦点分别为F1,F2,点P 在椭圆上运动, ![]() 的最大值为m,
的最大值为m, ![]() 的最小值为n,且m≥2n,则该椭圆的离心率的取值范围为________
的最小值为n,且m≥2n,则该椭圆的离心率的取值范围为________
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解甲、乙两厂的产品质量,采用分层抽样的方法从甲、乙两厂生产的产品中分别抽取14件和5件,测量产品中的微量元素x,y的含量(单位:毫克).下表是乙厂的5件产品的测量数据:
编号 | 1 | 2 | 3 | 4 | 5 |
x | 169 | 178 | 166 | 175 | 180 |
y | 75 | 80 | 77 | 70 | 81 |
已知甲厂生产的产品共有98件.
(1)求乙厂生产的产品数量;
(2)当产品中的微量元素x,y满足x≥175,且y≥75时,该产品为优等品,用上述样本数据估计乙厂生产的优等品的数量;
(3)从乙厂抽出的上述5件产品中,随机抽取2件,求抽取的2件产品中优等品数![]() 的分布列及其均值(即数学期望).
的分布列及其均值(即数学期望).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分13分)已知函数![]() (
(![]() 为常数,
为常数,![]() )
)
(1)若![]() 是函数
是函数![]() 的一个极值点,求
的一个极值点,求![]() 的值;
的值;
(2)求证:当![]() 时,
时,![]() 在
在![]() 上是增函数;
上是增函数;
(3)若对任意的![]() ,总存在
,总存在![]() ,使不等式
,使不等式![]() 成立,求正实数
成立,求正实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com