
已知![]() ,其中向量
,其中向量![]() =(
=(![]() ),
),![]() =(1,
=(1,![]() )(
)(![]() )
)
(1)求![]() 的单调递增区间;w.w.w.k.s.5.u.c.o.m
的单调递增区间;w.w.w.k.s.5.u.c.o.m ![]()
![]()
科目:高中数学 来源:浙江省瑞安市十校2012届高三上学期期中联考数学文科试题 题型:044
已知两个向量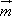 =(cos
=(cos![]() ,sin
,sin![]() ),
),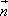 =(2
=(2![]() +sin
+sin![]() ,2
,2![]() -cos
-cos![]() ),其中
),其中![]() ∈(-
∈(-![]()
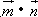 =1.
=1.
(Ⅰ)求sin(![]() +
+![]() )的值;
)的值;
(Ⅱ)求cos(![]() +
+![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分12分)已知![]() ,其中向量
,其中向量![]() =(
=(![]() ),
),![]() =(1,
=(1,![]() )(
)(![]() )(1)求
)(1)求![]() 的最小正周期;(2)在△ABC中,角A、B、C的对边分别为
的最小正周期;(2)在△ABC中,角A、B、C的对边分别为![]() 、
、![]() 、
、![]() ,
,![]() ,
,![]() ,
,![]() ,求边长b的值.
,求边长b的值.
查看答案和解析>>
科目:高中数学 来源:2012届安徽省六校教育研究会高三测试文科数学 题型:解答题
(本小题满分12分)已知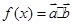 ,其中向量
,其中向量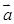 =
= ,
,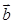 =
=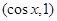 (x∈R)
(x∈R)
(Ⅰ)求f (x)的周期和单调递减区间;
(Ⅱ)在△ABC中,角A、B、C的对边分别为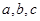 ,
,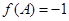 ,
,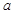 =
=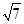 ,
,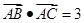 ,求边长b和c的值(b>c)。
,求边长b和c的值(b>c)。
查看答案和解析>>
科目:高中数学 来源: 题型:
已知![]() ,其中向量
,其中向量![]() =
=![]() ,
,![]() =
=![]() (x∈R)
(x∈R)
(Ⅰ)求f (x)的周期和单调递减区间;
(Ⅱ)在△ABC中,角A、B、C的对边分别为![]() ,
,![]() ,
,![]() =
=![]() ,
,![]() ,求边长b和c的值(b>c)。
,求边长b和c的值(b>c)。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com