
【题目】镇江市长江路江边春江潮广场要设计一尊鼎型塑像(如图1),塑像总高度为12米,塑像由两部分组成,上半部分由四根垂直于水平地面的等高垂直立柱组成(立柱上凸起部分忽略不计),下半部分由正四棱台的上底面四根水平横柱和正四棱台的四根侧棱斜柱组成,如图2所示.设计要求正棱台的水平横柱长度为4米,下底面边长为8米,设斜柱与地面的所成的角为![]() .
.

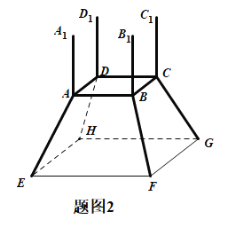
(1)用![]() 表示塑像上半部分立柱的高度,并求
表示塑像上半部分立柱的高度,并求![]() 的取值范围?
的取值范围?
(2)若该塑像上半部分立柱的造价为![]() 千元/米(立柱上凸起部分忽略不计),下半部分横柱和斜柱的造价都为2千元/米,问当
千元/米(立柱上凸起部分忽略不计),下半部分横柱和斜柱的造价都为2千元/米,问当![]() 为何值时,塑像总造价最低?
为何值时,塑像总造价最低?
科目:高中数学 来源: 题型:
【题目】新冠来袭,湖北告急!有一支援鄂医疗小队由3名医生和6名护士组成,他们全部要分配到三家医院.每家医院分到医生1名和护士1至3名,其中护士甲和护士乙必须分到同一家医院,则不同的分配方法有( )种
A.252B.540C.792D.684
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,曲线C1的参数方程为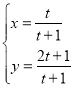 (t为参数),曲线C2的参数方程为
(t为参数),曲线C2的参数方程为![]() (α为参数),以坐标原点为极点.x轴正半轴为极轴建立极坐标系.
(α为参数),以坐标原点为极点.x轴正半轴为极轴建立极坐标系.
(Ⅰ)求曲线C1的普通方程和曲线C2的极坐标方程;
(Ⅱ)射线![]() 与曲线C2交于O,P两点,射线
与曲线C2交于O,P两点,射线![]() 与曲线C1交于点Q,若△OPQ的面积为1,求|OP|的值.
与曲线C1交于点Q,若△OPQ的面积为1,求|OP|的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
,![]() 是椭圆
是椭圆![]() :
:![]() 的左、右焦点,离心率为
的左、右焦点,离心率为![]() ,
,![]() ,
,![]() 是平面内两点,满足
是平面内两点,满足![]() ,线段
,线段![]() 的中点
的中点![]() 在椭圆上,
在椭圆上,![]() 周长为12.
周长为12.
(1)求椭圆![]() 的方程;
的方程;
(2)若过![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() ,求
,求![]() (其中
(其中![]() 为坐标原点)的取值范围.
为坐标原点)的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数f(x)若存在x0∈R,f(x0)=x0成立,则称x0为f(x)的不动点.已知f(x)=ax2+(b+1)x+b-1(a≠0).
(1)当a=1,b=-2时,求函数f(x)的不动点;
(2)若对任意实数b,函数f(x)恒有两个相异的不动点,求a的取值范围;
(3)在(2)的条件下,若y=f(x)图象上A,B两点的横坐标是函数f(x)的不动点,且A,B两点关于直线y=kx+![]() 对称,求b的最小值.
对称,求b的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了让居民了解垃圾分类,养成垃圾分类的习惯,让绿色环保理念深入人心.某市将垃圾分为四类:可回收物,餐厨垃圾,有害垃圾和其他垃圾.某班按此四类由![]() 位同学组成四个宣传小组,其中可回收物宣传小组有
位同学组成四个宣传小组,其中可回收物宣传小组有![]() 位同学,其余三个宣传小组各有
位同学,其余三个宣传小组各有![]() 位同学.现从这
位同学.现从这![]() 位同学中选派
位同学中选派![]() 人到某小区进行宣传活动,则每个宣传小组至少选派
人到某小区进行宣传活动,则每个宣传小组至少选派![]() 人的概率为( )
人的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小明每天从家步行去学校,有两条路线可以选择,第一条路线,需走天桥,不用等红灯,平均用时910秒;第二条路线,要经过两个红绿灯路口,如图,A处为小明家,D处为学校,走路段![]() 需240秒,在B处有一红绿灯,红灯时长120秒,绿灯时长30秒,走路段
需240秒,在B处有一红绿灯,红灯时长120秒,绿灯时长30秒,走路段![]() 需450秒,在C处也有一红绿灯,红灯时长100秒,绿灯时长50秒,走路段
需450秒,在C处也有一红绿灯,红灯时长100秒,绿灯时长50秒,走路段![]() 需200秒.小明进行了60天的试验,每天都选择第二条路线,并记录了在B处等待红灯的时长,经统计,60天中有48天在B处遇到红灯,根据记录的48天等待红灯时长的数据绘制了下面的频率分布直方图.已知B处和C处的红灯亮起的时刻恰好始终保持相同,且红绿灯之间切换无时间间隔.
需200秒.小明进行了60天的试验,每天都选择第二条路线,并记录了在B处等待红灯的时长,经统计,60天中有48天在B处遇到红灯,根据记录的48天等待红灯时长的数据绘制了下面的频率分布直方图.已知B处和C处的红灯亮起的时刻恰好始终保持相同,且红绿灯之间切换无时间间隔.

(1)若小明选择第二条路线,设当小明到达B处的时刻为B处红灯亮起后的第x秒(![]() )时,小明在B处等待红灯的时长为y秒,求y关于x的函数的解析式;
)时,小明在B处等待红灯的时长为y秒,求y关于x的函数的解析式;
(2)若小明选择第二条路线,请估计小明在B处遇到红灯的概率,并问小明是否可能在B处和C处都遇到红灯;
(3)若取区间中点作为该区间对应的等待红灯的时长,以这两条路线的平均用时作为决策依据,小明应选择哪一条路线?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】袋子A和B中装有若干个均匀的红球和白球,从A中摸出一个红球的概率是![]() ,从B中摸出一个红球的概率为p.
,从B中摸出一个红球的概率为p.
(1)从A中有放回地摸球,每次摸出一个,有3次摸到红球即停止.求恰好摸5次停止的概率;
(2)若A,B两个袋子中的球数之比为![]() ,将A,B中的球装在一起后,从中摸出一个红球的概率是
,将A,B中的球装在一起后,从中摸出一个红球的概率是![]() ,求p的值.
,求p的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com