练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    如图平面SAC⊥平面ACB，ΔSAC是边长为4的等边三角形，ΔACB为直角三角形，∠ACB=90°，BC=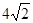，求二面角S-AB-C的余弦值。

     

    【答案】

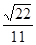
    【解析】

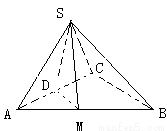
    试题分析：过S点作SD⊥AC于D，过D作DM⊥AB于M，连SM

    ∵平面SAC⊥平面ACB

    ∴SD⊥平面ACB

    ∴SM⊥AB

    又∵DM⊥AB

    ∴∠DMS为二面角S-AB-C的平面角

    在ΔSAC中SD=4×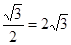

    在ΔACB中过C作CH⊥AB于H

    ∵AC=4，BC=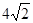

    ∴AB=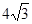

    ∵S=1/2AB·CH=1/2AC·BC

    ∴CH=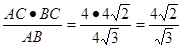

    ∵DM∥CH且AD=DC

    ∴DM=1/2CH=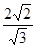

    ∵SD⊥平面ACB     DMÌ平面ACB

    ∴SD⊥DM

    在RTΔSDM中

    SM===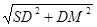

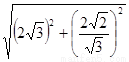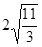
    ∴cos∠DMS===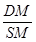

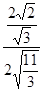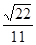
    考点：线面垂直关系及二面角

    点评：先作出二面角的平面角。由面面垂直可得线面垂直，作SD⊥平面ACB，然后利用三垂线定理作出二面角的平面角

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    如图平面SAC⊥平面ACB，△SAC是边长为4的等边三角形，△ACB为直角三角形，∠ACB=90°，BC=4
    		2
    ，求二面角S-AB-C的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图平面SAC⊥平面ACB，ΔSAC是边长为4的等边三角形，ΔACB为直角三角形，∠ACB=90°，BC=，求二面角S-AB-C的余弦值。

    查看答案和解析>>

    科目：高中数学 来源：2015届江苏省高一下学期期末考试数学试卷（解析版） 题型：解答题

    如图平面SAC⊥平面ACB，ΔSAC是边长为4的等边三角形，ΔACB为直角三角形，∠ACB=90°，BC=，求二面角S-AB-C的余弦值。

     

    查看答案和解析>>

    科目：高中数学 来源：2012-2013学年山东省聊城市四县六校联考高一（下）期末数学试卷（解析版） 题型：解答题

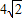    如图平面SAC⊥平面ACB，△SAC是边长为4的等边三角形，△ACB为直角三角形，∠ACB=90°，BC=，求二面角S-AB-C的余弦值．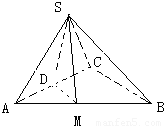

    查看答案和解析>>

    同步练习册答案