
【题目】在几何体![]() 中,底面
中,底面![]() 为菱形,
为菱形,![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() ,四边形
,四边形![]() 为直角梯形,
为直角梯形,![]() ,面
,面![]() 面
面![]() .
.
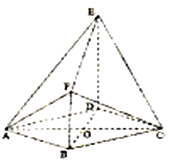
(1)证明:面![]() 面
面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)详见解析;(2)![]() .
.
【解析】
(1)由底面![]() 为菱形,可得
为菱形,可得![]() ,结合面面垂直的性质可得
,结合面面垂直的性质可得![]() 平面
平面![]() ,从而得到
,从而得到![]() ,又
,又![]() ,得到
,得到![]() 平面
平面![]() ,利用勾股定理证得
,利用勾股定理证得![]() ,由线面垂直的判定定理证得
,由线面垂直的判定定理证得![]() 平面
平面![]() ,利用面面垂直的判定定理证得平面
,利用面面垂直的判定定理证得平面![]() 平面
平面![]() ;
;
(2)取EF中点G,由题意可知,![]() ,则
,则![]() 平面
平面![]() ,分别以OA,OB,OG所在直线为
,分别以OA,OB,OG所在直线为![]() 轴建立空间直角坐标系
轴建立空间直角坐标系![]() ,分别求出平面AFC与平面AEC的一个法向量,由两法向量所成角的余弦值可得二面角
,分别求出平面AFC与平面AEC的一个法向量,由两法向量所成角的余弦值可得二面角![]() 的余弦值.
的余弦值.
(1)因为底面![]() 为菱形,所以
为菱形,所以![]() ,
,
又平面![]() 底面
底面![]() ,平面
,平面![]() 平面
平面![]() ,
,
因此![]() 平面
平面![]() ,从而
,从而![]() .
.
又![]() ,所以
,所以![]() 平面
平面![]() ,
,
由![]() ,
,
可知![]() ,
,
从而![]() ,故
,故![]() ,
,
又![]() ,所以
,所以![]() 平面
平面![]() .
.
又![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() .
.
(2)取![]() 中点
中点![]() ,由题可知
,由题可知![]() ,所以
,所以![]() 平面
平面![]() ,
,
又在菱形![]() 中,
中,![]() ,
,
分别以![]() 的方向为
的方向为![]() 轴正方向建立空间直角坐标系
轴正方向建立空间直角坐标系![]() (如图示),
(如图示),
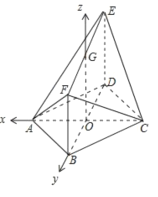
则![]() .
.
所以![]() ,
,
![]() ,
,
![]() .
.
由(1)可知![]() 平面
平面![]() ,所以平面
,所以平面![]() 的法向量可取为
的法向量可取为![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,则
,则 ,
,
即![]() ,
,
即![]() ,
,
令![]() ,得
,得![]() ,所以
,所以![]() .
.
从而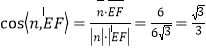 .由图可知,所求二面角的大小为锐角,
.由图可知,所求二面角的大小为锐角,
故所求的二面角![]() 的余弦值为
的余弦值为![]() .
.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:高中数学 来源: 题型:
【题目】已知四边形![]() 是矩形,
是矩形,![]() ,将
,将![]() 沿着对角线AC翻折,得到
沿着对角线AC翻折,得到![]() ,设顶点
,设顶点![]() 在平面
在平面![]() 上的投影为O.
上的投影为O.
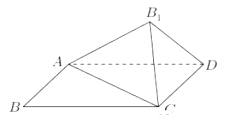
(1)若点O恰好落在边AD上,①求证:![]() 平面
平面![]() ;②若
;②若![]() ,
,![]() ,当BC取到最小值时,求k的值;
,当BC取到最小值时,求k的值;
(2)当![]() 时,若点O恰好落在
时,若点O恰好落在![]() 的内部(不包括边界),求二面角
的内部(不包括边界),求二面角![]() 的余弦值的取值范围.
的余弦值的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() .
.
(1)若![]() 在区间
在区间![]() 上不是单调函数,求实数
上不是单调函数,求实数![]() 的范围;
的范围;
(2)若对任意![]() ,都有
,都有![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)当![]() 时,设
时,设![]() ,对任意给定的正实数
,对任意给定的正实数![]() ,曲线
,曲线![]() 上是否存在两点
上是否存在两点![]() ,
,![]() ,使得
,使得![]() 是以
是以![]() (
(![]() 为坐标原点)为直角顶点的直角三角形,而且此三角形斜边中点在
为坐标原点)为直角顶点的直角三角形,而且此三角形斜边中点在![]() 轴上?请说明理由.
轴上?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形ABCD是边长为1的正方形,MD⊥ABCD,NB⊥ABCD.且MD=NB=1.则下列结论中:
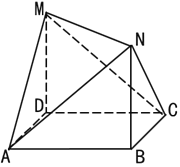
①MC⊥AN
②DB∥平面AMN
③平面CMN⊥平面AMN
④平面DCM∥平面ABN
所有假命题的个数是( )
A.0B.1C.2D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点A(x1,y1),D(x2,y2)其中(x1<x2)是曲线y2=9x(y≥0).上的两点,A,D两点在x轴上的射影分别为点B,C且|BC|=3.
(Ⅰ)当点B的坐标为(1,0)时,求直线AD的方程:
(Ⅱ)记△AOD的面积为S1,梯形ABCD的面积为S2,求![]() 的范围
的范围
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,平面四边形![]() 中,
中,![]() ,
,![]() 是
是![]() ,
,![]() 中点,
中点,![]() ,
,![]() ,
,![]() ,将
,将![]() 沿对角线
沿对角线![]() 折起至
折起至![]() ,使平面
,使平面![]() 平面
平面![]() ,则四面体
,则四面体![]() 中,下列结论不正确的是( )
中,下列结论不正确的是( )
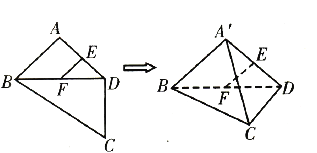
A. ![]() 平面
平面![]()
B. 异面直线![]() 与
与![]() 所成的角为
所成的角为![]()
C. 异面直线![]() 与
与![]() 所成的角为
所成的角为![]()
D. 直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
, ![]() ,其中
,其中![]() 是自然常数,
是自然常数, ![]() .
.
(1)当![]() 时,求
时,求![]() 的极值,并证明
的极值,并证明![]() 恒成立;
恒成立;
(2)是否存在实数![]() ,使
,使![]() 的最小值为
的最小值为![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区高考实行新方案,规定:语文、数学和英语是考生的必考科目,考生还须从物理、化学、生物、历史、地理和政治六个科目中选出了三个科目作为选考科目.若一名学生从六个科目中选出了三个科目作为选考科目,则称该学生的选考方案确定;否则,称该学生选考方案待确定.某学校为了了解高一年级200名学生选考科目的意向,随机选取20名学生进行了一次调查,统计选考科目人数如下表:
性别 | 选考方案确定情况 | 物理 | 化学 | 生物 | 历史 | 地理 | 政治 |
男生 | 选考方案确定的有5人 | 5 | 5 | 2 | 1 | 2 | 0 |
选考方案待确定的有7人 | 6 | 4 | 3 | 2 | 4 | 2 | |
女生 | 选考方案确定的有6人 | 3 | 5 | 2 | 3 | 3 | 2 |
选考方案待确定的有2人 | 1 | 2 | 1 | 0 | 1 | 1 |
(1)在选考方案确定的男生中,同时选考物理、化学、生物的人数有多少?
(2)从选考方案确定的男生中任选2名,试求出这2名学生选考科目完全相同的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在四棱锥P-ABCD中,底面四边形ABCD是菱形,AC∩BD=O,△PAC是边长为2的等边三角形,![]() .
.
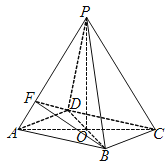
(1)求四棱锥P-ABCD的体积VP-ABCD;
(2)在线段PB上是否存在一点M,使得CM∥平面BDF?如果存在,求![]() 的值,如果不存在,请说明理由.
的值,如果不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com