
【题目】某公司生产的某批产品的销售量![]() 万件(生产量与销售量相等)与促销费用
万件(生产量与销售量相等)与促销费用![]() 万元满足
万元满足![]() (其中
(其中![]() ,
,![]() 为正常数).已知生产该产品还需投入成本
为正常数).已知生产该产品还需投入成本![]() 万元(不含促销费用),产品的销售价格定为
万元(不含促销费用),产品的销售价格定为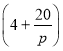 元
元![]() 件.
件.
(1)将该产品的利润![]() 万元表示为促销费用
万元表示为促销费用![]() 万元的函数;
万元的函数;
(2)促销费用投入多少万元时,该公司的利润最大?
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】2019年11月18日国际射联步手枪世界杯总决赛在莆田市综合体育馆开幕,这是国际射联步手枪世界杯总决赛时隔10年再度走进中国.为了增强趣味性,并实时播报现场赛况,我校现场小记者李明和播报小记者王华设计了一套播报转码法,发送方由明文→密文(加密),接受方由密文→明文(解密),已知加密的方法是:密码把英文的明文(真实文)按字母分解,其中英文的![]() 的26个字母(不论大小写)依次对应1,2,3,…,26这26个自然数通过变换公式:
的26个字母(不论大小写)依次对应1,2,3,…,26这26个自然数通过变换公式: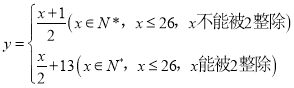 ,将明文转换成密文,如
,将明文转换成密文,如![]() ,即
,即![]() 变换成
变换成![]() ,即
,即![]() 变换成
变换成![]() .若按上述规定,若王华收到的密文是
.若按上述规定,若王华收到的密文是![]() ,那么原来的明文是( )
,那么原来的明文是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为弘扬中华民族优秀传统文化,树立正确的价值导向,落实立德树人根本任务,某市组织30000名高中学生进行古典诗词知识测试,根据男女学生人数比例,使用分层抽样的方法从中随机抽取100名学生,记录他们的分数,整理所得频率分布直方图如图:
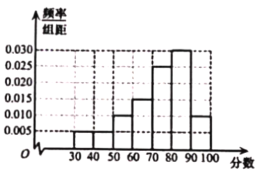
(Ⅰ)规定成绩不低于60分为及格,不低于85分为优秀,试估计此次测试的及格率及优秀率;
(Ⅱ)试估计此次测试学生成绩的中位数;
(Ⅲ)已知样本中有![]() 的男生分数不低于80分,且样本中分数不低于80分的男女生人数相等,试估计参加本次测试30000名高中生中男生和女生的人数.
的男生分数不低于80分,且样本中分数不低于80分的男女生人数相等,试估计参加本次测试30000名高中生中男生和女生的人数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知平面直角坐标系中,直线l的参数方程为![]() 为参数
为参数![]() ,以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为
,以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为![]() .
.
(1)求直线l的普通方程以及曲线C的参数方程;
(2)过曲线C上任意一点E作与直线l的夹角为![]() 的直线,交l于点F,求
的直线,交l于点F,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】自由购是一种通过自助结算购物的形式.某大型超市为调查顾客自由购的使用情况,随机抽取了100人,调查结果整理如下:
20以下 | [20,30) | [30,40) | [40,50) | [50,60) | [60,70] | 70以上 | |
使用人数 | 3 | 12 | 17 | 6 | 4 | 2 | 0 |
未使用人数 | 0 | 0 | 3 | 14 | 36 | 3 | 0 |
(1)现随机抽取1名顾客,试估计该顾客年龄在[30,50)且未使用自由购的概率;
(2)从被抽取的年龄在[50,70]使用的自由购顾客中,随机抽取2人进一步了解情况,求这2人年龄都在[50,60)的概率;
(3)为鼓励顾客使用自由购,该超市拟对使用自由购顾客赠送1个环保购物袋.若某日该超市预计有5000人购物,试估计该超市当天至少应准备多少个环保购物袋?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“一带一路”近年来成为了百姓耳熟能详的热门词汇,对于旅游业来说,“一带一路”战略的提出,让“丝路之旅”超越了旅游产品、旅游线路的简单范畴,赋予了旅游促进跨区域融合的新理念. 而其带来的设施互通、经济合作、人员往来、文化交融更是将为相关区域旅游发展带来巨大的发展机遇.为此,旅游企业们积极拓展相关线路;各地旅游主管部门也在大力打造丝路特色旅游品牌和服务.某市旅游局为了解游客的情况,以便制定相应的策略. 在某月中随机抽取甲、乙两个景点10天的游客数,统计得到茎叶图如下:

(1)若将图中景点甲中的数据作为该景点较长一段时期内的样本数据,以每天游客人数频率作为概率.今从这段时期内任取4天,记其中游客数超过130人的天数为![]() ,求概率
,求概率![]() ;
;
(2)现从上图20天的数据中任取2天的数据(甲、乙两景点中各取1天),记其中游客数不低于125且不高于135人的天数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,函数
,函数![]() .
.
(1)求实数![]() 的值,使得
的值,使得![]() 为奇函数;
为奇函数;
(2)若关于![]() 的方程
的方程![]() 有两个不同实数解,求
有两个不同实数解,求![]() 的取值范围;
的取值范围;
(3)若关于![]() 的不等式
的不等式![]() 对任意
对任意![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设点![]() ,
,![]() 的坐标分别为
的坐标分别为![]() ,
,![]() ,直线
,直线![]() 和
和![]() 相交于点
相交于点![]() ,且
,且![]() 和
和![]() 的斜率之差是1.
的斜率之差是1.
(1)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)过轨迹![]() 上的点
上的点![]() ,
,![]() ,作圆
,作圆![]() :
:![]() 的两条切线,分别交
的两条切线,分别交![]() 轴于点
轴于点![]() ,
,![]() .当
.当![]() 的面积最小时,求
的面积最小时,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com