
ЁОЬтФПЁПДѓбЇЩњедУєРћгУКЎМйВЮМгЩчЛсЪЕМљЃЌЖдЛњаЕЯњЪлЙЋЫО7дТЗнжС12дТЗнЯњЪлФГжжЛњаЕХфМўЕФЯњЪлСПМАЯњЪлЕЅМлНјааСЫЕїВщЃЌЯњЪлЕЅМл![]() КЭЯњЪлСП
КЭЯњЪлСП![]() жЎМфЕФвЛзщЪ§ОнШчЯТБэЫљЪОЃК
жЎМфЕФвЛзщЪ§ОнШчЯТБэЫљЪОЃК
дТЗн | 7 | 8 | 9 | 10 | 11 | 12 |
ЯњЪлЕЅМл | 9 | 9.5 | 10 | 10.5 | 11 | 8 |
ЯњЪлСП | 11 | 10 | 8 | 6 | 5 | 14 |
ЃЈ1ЃЉИљОн7жС11дТЗнЕФЪ§ОнЃЌЧѓГі![]() Йигк
Йигк![]() ЕФЛиЙщжБЯпЗНГЬЃЛ
ЕФЛиЙщжБЯпЗНГЬЃЛ
ЃЈ2ЃЉШєгЩЛиЙщжБЯпЗНГЬЕУЕНЕФЙРМЦЪ§ОнгыЪЃЯТЕФМьбщЪ§ОнЕФЮѓВюВЛГЌЙ§0.5дЊЃЌдђШЯЮЊЫљЕУЕНЕФЛиЙщжБЯпЗНГЬЪЧРэЯыЕФЃЌЪдЮЪЃЈ1ЃЉжаЫљЕУЕНЕФЛиЙщжБЯпЗНГЬЪЧЗёРэЯыЃП
ЃЈ3ЃЉдЄМЦдкНёКѓЕФЯњЪлжаЃЌЯњЪлСПгыЯњЪлЕЅМлШдШЛЗўДгЃЈ1ЃЉжаЕФЙиЯЕЃЌШєИУжжЛњЦїХфМўЕФГЩБОЪЧ2.5дЊ/МўЃЌФЧУДИУХфМўЕФЯњЪлЕЅМлгІЖЈЮЊЖрЩйдЊВХФмЛёЕУзюДѓРћШѓЃПЃЈзЂЃКРћШѓ=ЯњЪлЪеШы-ГЩБОЃЉЃЎ
ЁЁВЮПМЙЋЪНЃКЛиЙщжБЯпЗНГЬ![]() ЃЌЦфжа
ЃЌЦфжа ЃЌВЮПМЪ§ОнЃК
ЃЌВЮПМЪ§ОнЃК ![]() ЃЎ
ЃЎ
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЈ2ЃЉПЩвдШЯЮЊЫљЕУЕНЕФЛиЙщжБЯпЗНГЬЪЧРэЯыЕФЃЈ3ЃЉВњЦЗЕФЯњЪлЕЅМлЖЈЮЊ7.5дЊ/МўЪБЃЌЛёЕУЕФРћШѓзюДѓЃЎ
ЃЈ2ЃЉПЩвдШЯЮЊЫљЕУЕНЕФЛиЙщжБЯпЗНГЬЪЧРэЯыЕФЃЈ3ЃЉВњЦЗЕФЯњЪлЕЅМлЖЈЮЊ7.5дЊ/МўЪБЃЌЛёЕУЕФРћШѓзюДѓЃЎ
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉИљОнЛиЙщжБЯпЗНГЬЙЋЪНЃЌЧѓ![]() ЃЌдђ
ЃЌдђ![]() ЃЌМДПЩЃЛЃЈ2ЃЉРћгУЛиЙщжБЯпЗНГЬЃЌЙРВт
ЃЌМДПЩЃЛЃЈ2ЃЉРћгУЛиЙщжБЯпЗНГЬЃЌЙРВт![]() ЪБЃЌ
ЪБЃЌ ![]() ЃЌМЦЫуЮѓВюШЗЖЈЪЧРэЯыФтКЯЃЛЃЈ3ЃЉаДГіЯњЪлРћШѓ
ЃЌМЦЫуЮѓВюШЗЖЈЪЧРэЯыФтКЯЃЛЃЈ3ЃЉаДГіЯњЪлРћШѓ![]() ЃЌРћгУОљжЕВЛЕШЪНЧѓзюДѓжЕЃЎ
ЃЌРћгУОљжЕВЛЕШЪНЧѓзюДѓжЕЃЎ
ЪдЬтНтЮіЃКЃЈ1ЃЉвђЮЊ![]() ЃЌ
ЃЌ
Ыљвд![]() ЃЌдђ
ЃЌдђ![]() ЃЌ
ЃЌ
гкЪЧ![]() Йигк
Йигк![]() ЕФЛиЙщжБЯпЗНГЬЮЊ
ЕФЛиЙщжБЯпЗНГЬЮЊ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЕБ![]() ЪБЃЌ
ЪБЃЌ ![]() ЃЌдђ
ЃЌдђ![]() ЃЌ
ЃЌ
ЫљвдПЩвдШЯЮЊЫљЕУЕНЕФЛиЙщжБЯпЗНГЬЪЧРэЯыЕФЃЛ
ЃЈ3ЃЉСюЯњЪлРћШѓЮЊ![]() ЃЌдђ
ЃЌдђ![]() ЃЌ
ЃЌ
вђЮЊ![]() ЃЌ
ЃЌ
ЕБЧвНіЕБ![]() ЃЌМД
ЃЌМД![]() ЪБЃЌ
ЪБЃЌ ![]() ШЁзюДѓжЕЃЎ
ШЁзюДѓжЕЃЎ
ЫљвдИУВњЦЗЕФЯњЪлЕЅМлЖЈЮЊ7ЃЎ5дЊ/МўЪБЃЌЛёЕУЕФРћШѓзюДѓЃЎ


 НЬВФШЋНтзжДЪОфЦЊЯЕСаД№АИ
НЬВФШЋНтзжДЪОфЦЊЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГаЃЮЊЛКНтИпШ§бЇЩњЕФИпПМбЙСІЃЌОГЃОйаавЛаЉаФРэЫижЪзлКЯФмСІбЕСЗЛюЖЏЃЌОЙ§вЛЖЮЪБМфЕФбЕСЗКѓДгИУФъМЖ800УћбЇЩњжаЫцЛњГщШЁ100УћбЇЩњНјааВтЪдЃЌВЂНЋЦфГЩМЈЗжЮЊ![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЮхИіЕШМЖЃЌЭГМЦЪ§ОнШчЭМЫљЪОЃЈЪгЦЕТЪЮЊИХТЪЃЉЃЌИљОнвдЩЯГщбљЕїВщЪ§ОнЃЌЛиД№ЯТСаЮЪЬтЃК
ЮхИіЕШМЖЃЌЭГМЦЪ§ОнШчЭМЫљЪОЃЈЪгЦЕТЪЮЊИХТЪЃЉЃЌИљОнвдЩЯГщбљЕїВщЪ§ОнЃЌЛиД№ЯТСаЮЪЬтЃК
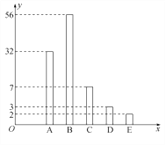
ЃЈ1ЃЉЪдЙРЫуИУаЃИпШ§ФъМЖбЇЩњЛёЕУГЩМЈЮЊ![]() ЕФШЫЪ§ЃЛ
ЕФШЫЪ§ЃЛ
ЃЈ2ЃЉШєЕШМЖ![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЗжБ№ЖдгІ100ЗжЁЂ90ЗжЁЂ80ЗжЁЂ70ЗжЁЂ60ЗжЃЌбЇаЃвЊЧѓЦНОљЗжДя90ЗжвдЩЯЮЊЁАПМЧАаФРэЮШЖЈећЬхЙ§ЙиЁБЃЌЧыЮЪИУаЃИпШ§ФъМЖФПЧАбЇЩњЕФЁАПМЧАаФРэЮШЖЈећЬхЁБЪЧЗёЙ§ЙиЃП
ЗжБ№ЖдгІ100ЗжЁЂ90ЗжЁЂ80ЗжЁЂ70ЗжЁЂ60ЗжЃЌбЇаЃвЊЧѓЦНОљЗжДя90ЗжвдЩЯЮЊЁАПМЧАаФРэЮШЖЈећЬхЙ§ЙиЁБЃЌЧыЮЪИУаЃИпШ§ФъМЖФПЧАбЇЩњЕФЁАПМЧАаФРэЮШЖЈећЬхЁБЪЧЗёЙ§ЙиЃП
ЃЈ3ЃЉЮЊСЫНтаФРэНЁПЕзДЬЌЮШЖЈбЇЩњЕФЬиЕуЃЌЯжДг![]() ЁЂ
ЁЂ![]() СНжжМЖБ№жаЃЌгУЗжВуГщбљЕФЗНЗЈГщШЁ11ИібЇЩњбљБОЃЌдйДгжаШЮвтбЁШЁ3ИібЇЩњбљБОЗжЮіЃЌЧѓет3ИібљБОЮЊ
СНжжМЖБ№жаЃЌгУЗжВуГщбљЕФЗНЗЈГщШЁ11ИібЇЩњбљБОЃЌдйДгжаШЮвтбЁШЁ3ИібЇЩњбљБОЗжЮіЃЌЧѓет3ИібљБОЮЊ![]() МЖЕФИіЪ§
МЖЕФИіЪ§![]() ЕФЗжВМСагыЪ§бЇЦкЭћ.
ЕФЗжВМСагыЪ§бЇЦкЭћ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвЛКажазАгаИїЩЋЧђ12жЛЃЌЦфжа5ИіКьЧђЃЌ4ИіКкЧђЃЌ2ИіАзЧђЃЌ1ИіТЬЧђЃЛДгжаЫцЛњШЁГі1ЧђЃЎЧѓЃК
ЃЈ1ЃЉШЁГіЕФ1ЧђЪЧКьЧђЛђКкЧђЕФИХТЪЃЛ
ЃЈ2ЃЉШЁГіЕФ1ЧђЪЧКьЧђЛђКкЧђЛђАзЧђЕФИХТЪЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§fЃЈxЃЉ=lnxЉ ![]() aЃЈxЉ1ЃЉЃЈaЁЪRЃЉЃЎ
aЃЈxЉ1ЃЉЃЈaЁЪRЃЉЃЎ
ЃЈ1ЃЉШєa=Љ2ЃЌЧѓЧњЯпy=fЃЈxЃЉдкЕуЃЈ1ЃЌfЃЈ1ЃЉЃЉДІЕФЧаЯпЗНГЬЃЛ
ЃЈ2ЃЉШєВЛЕШЪНfЃЈxЃЉЃМ0ЖдШЮвтxЁЪЃЈ1ЃЌ+ЁоЃЉКуГЩСЂЃЎ ЃЈЂЁЃЉЧѓЪЕЪ§aЕФШЁжЕЗЖЮЇЃЛ
ЃЈЂЂЃЉЪдБШНЯeaЉ2гыaeЉ2ЕФДѓаЁЃЌВЂИјГіжЄУїЃЈeЮЊздШЛЖдЪ§ЕФЕзЪ§ЃЌe=2.71828ЃЉЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊХзЮяЯп![]() ЃК
ЃК ![]() ЕФНЙЕу
ЕФНЙЕу![]() вВЪЧЭждВ
вВЪЧЭждВ![]() ЃК
ЃК ![]() ЃЈ
ЃЈ![]() ЃЉЕФвЛИіНЙЕуЃЌ
ЃЉЕФвЛИіНЙЕуЃЌ ![]() гы
гы![]() ЕФЙЋЙВЯвГЄЮЊ
ЕФЙЋЙВЯвГЄЮЊ![]() .
.
ЃЈЂёЃЉЧѓ![]() ЕФЗНГЬ
ЕФЗНГЬ
ЃЈЂђЃЉЙ§Еу![]() ЕФжБЯп
ЕФжБЯп![]() гы
гы![]() ЯрНЛгк
ЯрНЛгк![]() ЃЌ
ЃЌ ![]() СНЕуЃЌгы
СНЕуЃЌгы![]() ЯрНЛгк
ЯрНЛгк![]() ЃЌ
ЃЌ ![]() СНЕуЃЌЧв
СНЕуЃЌЧв![]() ЃЌ
ЃЌ ![]() ЭЌЯђ.Шє
ЭЌЯђ.Шє![]() ЧѓжБЯп
ЧѓжБЯп![]() ЕФаБТЪЃЛ
ЕФаБТЪЃЛ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊжБЯпl1ЃКx+my+6=0ЃЌl2ЃКЃЈmЉ2ЃЉx+3y+2m=0ЃЌЧѓЃК
ЃЈ1ЃЉШєl1ЁЭl2 ЃЌ ЧѓmЕФжЕЃЛ
ЃЈ2ЃЉШєl1ЁЮl2 ЃЌ ЧѓmЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЫФУцЬхABCDжаЃЌABКЭCDЮЊЖдРтЃЎЩшAB=aЃЌCD=bЃЌЧввьУцжБЯпABгыCDМфЕФОрРыЮЊdЃЌМаНЧЮЊІШЃЎ
ЃЈЂёЃЉШєІШ= ![]() ЃЌЧвРтABДЙжБгкЦНУцBCDЃЌЧѓЫФУцЬхABCDЕФЬхЛ§ЃЛ
ЃЌЧвРтABДЙжБгкЦНУцBCDЃЌЧѓЫФУцЬхABCDЕФЬхЛ§ЃЛ
ЃЈЂђЃЉЕБІШ= ![]() ЪБЃЌжЄУїЃКЫФУцЬхABCDЕФЬхЛ§ЮЊвЛЖЈжЕЃЛ
ЪБЃЌжЄУїЃКЫФУцЬхABCDЕФЬхЛ§ЮЊвЛЖЈжЕЃЛ
ЃЈЂѓЃЉЧѓЫФУцЬхABCDЕФЬхЛ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкГЄЗНЬхABCDЉA1B1C1D1жаЃЌAB=2BB1=2BCЃЌEЮЊD1C1ЕФжаЕуЃЌСЌНсEDЃЌECЃЌEBКЭDBЃЎ
ЃЈЂёЃЉжЄУїЃКA1D1ЁЮЦНУцEBCЃЛ
ЃЈЂђЃЉжЄУїЃКЦНУцEDBЁЭЦНУцEBCЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§![]() ЃЌжБЯп
ЃЌжБЯп![]() .
.
ЃЈ1ЃЉШєжБЯп![]() гыЧњЯп
гыЧњЯп![]() гаЧвНігавЛИіЙЋЙВЕуЃЌЧѓЙЋЙВЕуКсзјБъЕФжЕЃЛ
гаЧвНігавЛИіЙЋЙВЕуЃЌЧѓЙЋЙВЕуКсзјБъЕФжЕЃЛ
ЃЈ2ЃЉШє![]() ЃЌЧѓжЄЃК
ЃЌЧѓжЄЃК ![]() .
.
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com