
分析 (1)根据圆的参数方程求出圆心坐标及半径,可得曲线C1的普通方程,
根据椭圆的标准方程,确定椭圆的长半轴和短半轴长,可得曲线C2的参数方程;
2)曲线C2上任意一点$Q(\sqrt{10}cosφ,sinφ)$到到圆心O(0,6)的距离$d=\sqrt{{{(\sqrt{10}cosφ-0)}^2}+{{(sinφ-6)}^2}}$,根据正弦型函数的图象和性质,可得|PQ|的最大值.
解答 解:(1)∵曲线C1:$\left\{\begin{array}{l}x=\sqrt{2}cosθ\\ y=6+\sqrt{2}sinθ\end{array}\right.$,(θ为参数),
∴曲线C1表示以(0,6)为圆心,$\sqrt{2}$为半径的圆,
故C1的普通方程为:x2+(y-6)2=2,
由曲线C2:$\frac{x^2}{10}+{y^2}=1$表示焦点在x轴上,长半轴为$\sqrt{10}$,短半轴为1的椭圆,
故C2的参数方程为:$\left\{\begin{array}{l}x=\sqrt{10}cosφ\\ y=sinφ\end{array}\right.$,(φ为参数) …(4分)
(2)曲线C2上任意一点$Q(\sqrt{10}cosφ,sinφ)$到到圆心O(0,6)的距离$d=\sqrt{{{(\sqrt{10}cosφ-0)}^2}+{{(sinφ-6)}^2}}$…(6分)
=$\sqrt{-9{{sin}^2}φ-12sinφ+46}=\sqrt{-9{{(sinφ+\frac{2}{3})}^2}+50}≤5\sqrt{2}$…(8分)
当$sinφ=-\frac{2}{3}$时,d取最大值$5\sqrt{2}$,
此时$|PQ{|_{max}}=5\sqrt{2}+\sqrt{2}=6\sqrt{2}$…(10分)
点评 本题考查的知识点是函数的最值及其几何意义,正弦型函数的图象和性质,参数方程与普通方程的互化,难度中档.


 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案科目:高中数学 来源: 题型:填空题
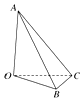 (理)如图在四面体OABC中,OA,OB,OC两两垂直,且OB=OC=3,OA=4,给出如下判断:
(理)如图在四面体OABC中,OA,OB,OC两两垂直,且OB=OC=3,OA=4,给出如下判断:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
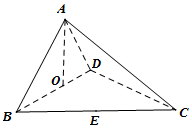 如图,在三棱锥A-BCD中,O、E分别为BD、BC中点,CA=CB=CD=BD=4,AB=AD=2$\sqrt{2}$
如图,在三棱锥A-BCD中,O、E分别为BD、BC中点,CA=CB=CD=BD=4,AB=AD=2$\sqrt{2}$查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)的图象关于直线x=$\frac{π}{2}$对称 | B. | f(x)的周期为π | ||
| C. | 若|f(x1)|=|f(x2)|,则x1=x2+2kπ(k∈Z) | D. | f(x)在区间[$\frac{π}{4}$,$\frac{3π}{4}$]上单调递减 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | 12 | C. | 24 | D. | 48 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|-3<x<-1} | B. | {x|2<x<3} | C. | {x|-3<x<-1或2<x<3} | D. | {x|-3<x<-2或1<x<3} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com