
(本题满分16分)
已知数列{an}满足Sn+an=2n+1,
(1) 写出a1, a2, a3,并推测an的表达式;
(2) 用数学归纳法证明所得的结论。
(1) a1=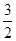 , a2=
, a2=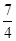 , a3=
, a3=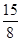 , 猜测 an=2-
, 猜测 an=2-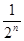 (2)见解析
(2)见解析
【解析】解: (1) a1=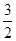 , a2=
, a2=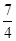 , a3=
, a3=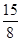 , 猜测 an=2-
, 猜测 an=2-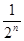 ……5分
……5分
(2) ①由(1)已得当n=1时,命题成立;……8分
②假设n=k时,命题成立,即 ak=2-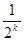 , ……10分
, ……10分
当n=k+1时, a1+a2+……+ak+ak+1+ak+1=2(k+1)+1,且a1+a2+……+ak=2k+1-ak
∴2k+1-ak+2ak+1=2(k+1)+1=2k+3,
∴2ak+1=2+2-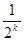 , ak+1=2-
, ak+1=2-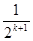 , 即当n=k+1时,命题成立. ……15分
, 即当n=k+1时,命题成立. ……15分
根据①②得n∈N+ , an=2-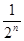 都成立
……16分
都成立
……16分
思路分析:第一问利用Sn+an=2n+1,递推得到a1=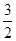 , a2=
, a2=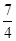 , a3=
, a3=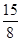 , 猜测 an=2-
, 猜测 an=2-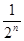
第二问中,1)已得当n=1时,命题成立;
②假设n=k时,命题成立,即 ak=2-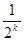 ,当n=k+1时, a1+a2+……+ak+ak+1+ak+1=2(k+1)+1,且a1+a2+……+ak=2k+1-ak
,当n=k+1时, a1+a2+……+ak+ak+1+ak+1=2(k+1)+1,且a1+a2+……+ak=2k+1-ak
∴2k+1-ak+2ak+1=2(k+1)+1=2k+3,
∴2ak+1=2+2-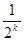 , ak+1=2-
, ak+1=2-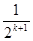
综上可知成立。


科目:高中数学 来源: 题型:
| a1+2a2+3a3+…+nan |
| 1+2+3+…+n |
| n(n+1)(2n+1) |
| 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:
(本题满分16分)本题共有2个小题,第1小题满分8分,第2小题满分8分.
已知函数![]() (
(![]() ,
,![]() 、
、![]() 是常数,且
是常数,且![]() ),对定义域内任意
),对定义域内任意![]() (
(![]() 、
、![]() 且
且![]() ),恒有
),恒有![]() 成立.
成立.
(1)求函数![]() 的解析式,并写出函数的定义域;
的解析式,并写出函数的定义域;
(2)求![]() 的取值范围,使得
的取值范围,使得![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
(本题满分16分)已知数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() .数列
.数列![]() 中,
中,![]() ,
,
![]()
![]() .(1)求数列
.(1)求数列![]() 的通项公式;(2)若存在常数
的通项公式;(2)若存在常数![]() 使数列
使数列![]() 是等比数列,求数列
是等比数列,求数列![]() 的通项公式;(3)求证:①
的通项公式;(3)求证:①![]() ;②
;②![]() .
.
查看答案和解析>>
科目:高中数学 来源:江苏省私立无锡光华学校2009—2010学年高二第二学期期末考试 题型:解答题
本题满分16分)已知圆内接四边形ABCD的边长分别为AB = 2,BC = 6,CD = DA = 4;求四边形ABCD的面积.
查看答案和解析>>
科目:高中数学 来源:2010年上海市徐汇区高三第二次模拟考试数学卷(文) 题型:解答题
(本题满分16分;第(1)小题5分,第(2)小题5分,第三小题6分)
已知函数 
(1)判断并证明 在
在 上的单调性;
上的单调性;
(2)若存在 ,使
,使 ,则称
,则称 为函数
为函数 的不动点,现已知该函数有且仅有一个不动点,求
的不动点,现已知该函数有且仅有一个不动点,求 的值;
的值;
(3)若 在
在 上恒成立 , 求
上恒成立 , 求 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com